Question

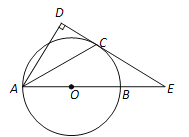
【题目】如图，直线y＝－x＋分别与x轴、y轴交于B、C两点，点A在x轴上，∠ACB＝90°,抛物线＝ax2＋bx＋经过A、B两点．

（1）求A、B两点的坐标；

（2）求抛物线的解析式；

（3）点M是直线BC上方抛物线上的一点，过点M从作MH⊥BC于点H，作轴MD∥y轴交BC于点D，求DMH周长的最大值．

Answer 1

【答案】(1) 点A的坐标为（－1，0）； (2) y＝－x2＋x＋ (3).

【解析】

试题(1)、根据直线的函数解析式求出点B和点C的坐标，然后根据△AOC和△COB相似得出点A的坐标；(2)、将点A和点B的坐标代入函数解析式，利用待定系数法求出函数解析式；(3)、由题意知，△DMH为直角三角形，且∠M＝30°，当MD取得最大值时，△DMH的周长最大；设出点M的坐标，从而得出点D的坐标，然后利用做差法得出MD的长度，利用函数的性质求出MD的最大值，从而根据特殊直角三角形的性质得出周长的最大值．

试题解析：解： (1)∵直线y＝－x＋；分别与x轴、y轴交于B、C两点，

∴点B的坐标为(3，0)，点C的坐标为(0，)；

∴∠ACO＋∠BCO＝90°，∠ACO＋∠CAO＝90°， ∴∠CAO＝∠BCO，

∵∠AOC＝∠COB＝90°， ∴△AOC∽△COB， ∴.∴＝，∴AO＝1，

∴点A的坐标为（－1，0）．

(2)∵抛物线y＝ax2＋bx＋；经过A、B两点，

∴，解得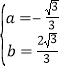：， ∴抛物线的解析式为y＝－x2＋x＋；

(3)由题意知，△DMH为直角三角形，且∠M＝30°，当MD取得最大值时，△DMH的周长最大．

设M(x，－x2＋x＋)， D(x，－x＋)， 则MD＝(－x2＋x＋)－(－x＋)，

即：MD＝－x2＋x(0＜x＜3)， MD＝－ (x－)2＋，

∴当x＝时，MD有最大值，

∴△DMH周长的最大值为＋×＋×＝．