ЬтФПФкШн
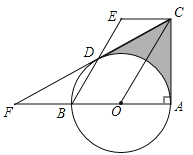
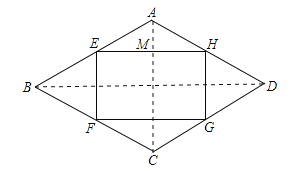
ЁОЬтФПЁПШчЭМЫљЪОЃЌбЇаЃзМБИаоНЈвЛИіКЌФкНгОиаЮЕФСтаЮЛЈЬГЃЈЛЈЬГЮЊжсЖдГЦЭМаЮЃЉЃЎОиаЮЕФЫФИіЖЅЕуЗжБ№дкСтаЮЫФЬѕБпЩЯЃЌСтаЮЕФИпAM=3УзЃЌЁЯABC=60ЁуЃЎЩшAE=xУзЃЈ1ЁмxЁм2ЃЉЃЌОиаЮEFGHЕФУцЛ§ЮЊSУз2ЃЎ
ЃЈ1ЃЉЧѓSгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉбЇаЃзМБИдкОиаЮФкжжжВКьЩЋЛЈВнЃЌдкЫФИіШ§НЧаЮФкжжжВТЬЩЋЛЈВнЃЎвбжЊЃККьЩЋКЭТЬЩЋжВЮяЕФМлИёЮЊ200дЊ/Уз2ЃЌ100дЊ/Уз2ЃЌЕБxЮЊКЮжЕЪБЃЌЙКТђЛЈЛмЫљашЕФзмЗбгУзюЕЭЃЌВЂЧѓГізюЕЭзмЗбгУЃЈНсЙћБЃСєИљКХЃЉЃЎ

ЁОД№АИЁПЃЈ1ЃЉS=-![]() x2+6xЃЈ2ЃЉ900
x2+6xЃЈ2ЃЉ900![]()
ЁОНтЮіЁП
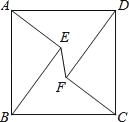
ЃЈ1ЃЉСЌНгACЁЂBDЃЌИљОнжсЖдГЦЕФаджЪЃЌПЩЕУEHЁЮBDЃЌEFЁЮACЃЌЁїBEFЮЊЕШБпШ§НЧаЮЃЌДгЖјЧѓГіEFЃЎдкRtЁїAEMжаЧѓГіEMЃЌМЬЖјЕУГіEHЃЌетбљМДПЩЕУГіSгыxЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ2ЃЉИљОнЃЈ1ЃЉЕФД№АИЃЌПЩЧѓГіЫФИіШ§НЧаЮЕФУцЛ§ЃЌЩшЗбгУЮЊWЃЌдђПЩЕУГіWЙигкxЕФЖўДЮКЏЪ§ЙиЯЕЪНЃЌРћгУХфЗНЗЈЧѓзюжЕМДПЩЃЎ
ЃЈ1ЃЉСЌНгACЁЂBDЃЎ
ЁпЛЈЬГЮЊжсЖдГЦЭМаЮЃЌЁрEHЁЮBDЃЌEFЁЮACЃЌЁрЁїBEFЁзЁїBACЃЎ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌЁрAB=BCЃЎ
гжЁпЁЯABC=60ЁуЃЌЁрЁїABCЪЧЕШБпШ§НЧаЮЃЎ
ЭЌРэЃЌЕУЕНЁїBEFЪЧЕШБпШ§НЧаЮЃЎ
ЁпAB=![]() =2
=2![]() ЃЌЁрEF=BE=ABЉAE=ЃЈ2
ЃЌЁрEF=BE=ABЉAE=ЃЈ2![]() ЉxЃЉmЃЎдкRtЁїAEMжаЃЌЁЯAEM=ЁЯABD=30ЁуЃЌдђEM=AEcosЁЯAEM=
ЉxЃЉmЃЎдкRtЁїAEMжаЃЌЁЯAEM=ЁЯABD=30ЁуЃЌдђEM=AEcosЁЯAEM=![]() xЃЌЁрEH=2EM=
xЃЌЁрEH=2EM=![]() xЃЌЙЪПЩЕУS=
xЃЌЙЪПЩЕУS=![]() xЃЈ2
xЃЈ2![]() ЉxЃЉ=Љ
ЉxЃЉ=Љ![]() x2+6xЃЛ
x2+6xЃЛ
ЃЈ2ЃЉЁпСтаЮABCDЕФУцЛ§ЮЊ2![]() ЁС3=6
ЁС3=6![]() ЃЌОиаЮEFGHЕФУцЛ§ЮЊЉ
ЃЌОиаЮEFGHЕФУцЛ§ЮЊЉ![]() x2+6xЃЌЁрЫФИіШ§НЧаЮЕФУцЛ§ЮЊ6
x2+6xЃЌЁрЫФИіШ§НЧаЮЕФУцЛ§ЮЊ6![]() +
+![]() x2Љ6xЃЌЩшзмЗбгУЮЊWЃЌдђW=200ЃЈЉ
x2Љ6xЃЌЩшзмЗбгУЮЊWЃЌдђW=200ЃЈЉ![]() x2+6xЃЉ+100ЃЈ6
x2+6xЃЉ+100ЃЈ6![]() +
+![]() x2Љ6xЃЉ
x2Љ6xЃЉ
=Љ100![]() x2+600x+600
x2+600x+600![]()
=Љ100![]() ЃЈxЉ
ЃЈxЉ![]() ЃЉ2+900
ЃЉ2+900![]() ЃЎ
ЃЎ
Ёп1ЁмxЁм2ЃЌЁрЕБx=![]() ЪБЃЌWШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ900
ЪБЃЌWШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ900![]() ЃЎ
ЃЎ
Д№ЃКЕБx=![]() ЪБЃЌЙКТђЛЈЛмЫљашЕФзмЗбгУзюЕЭЃЌзюЕЭзмЗбгУ900
ЪБЃЌЙКТђЛЈЛмЫљашЕФзмЗбгУзюЕЭЃЌзюЕЭзмЗбгУ900![]() ЃЎ
ЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ