题目内容
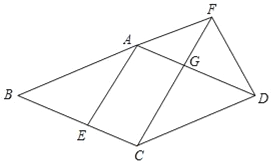
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.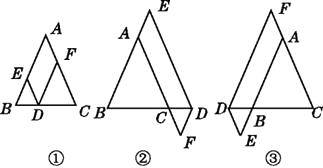
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③.请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF=.
【答案】
(1)证明:∵DE∥AC,DF∥AB,
∴∠FDC=∠B,四边形AEDF是平行四边形.
∴DE=AF.
又∵AB=AC,∴∠B=∠C,
∴∠FDC=∠C,∴DF=FC,
∴DE+DF=AF+FC=AC
(2)解:当点D在边BC的延长线上时,DE-DF=AC;
∵DE∥AC,DF∥AB,
∴∠FDC=∠B,四边形AEDF是平行四边形.
∴DE=AF.
又∵AB=AC,∴∠B=∠ACB,
∴∠FDC=∠ACB,
∵∠DCF=∠ACB,
∴∠FDC=∠DCF
∴DF=FC,
∴AC+CF=AC+DF=AF=DE
DE-DF=AC;
同理可证当点D在边BC的反向延长线上时,DF-DE=AC
(3)2或10
【解析】(3)根据(1)的结论DE+DF=AC
∵AC=6,DE=4
∴DF=AC-DE=6-4=2
根据图②的结论DE-DF=AC
∴DF=DE-AC=-2,不符合题意;
根据图③的结论DF-DE=AC
∴DF=DE+AC=4+6=10
(1)根据已知条件及平行四边形的判定,可证明四边形AEDF是平行四边形,得出DE=AF,再根据等腰三角形的性质及平行线的性质证明∠FDC=∠C,得到DF=FC,然后根据DE+DF=AF+FC,即可证得结论。
(2)图②根据已知条件及平行四边形的判定,可证明四边形AEDF是平行四边形,得出DE=AF,再根据等腰三角形的性质及平行线的性质证明∠FDC=∠DCF,得到DF=FC,然后根据AC+CF=AC+DF=AF=DE,即可证得结论;同理可得出图③的结论。
(3)利用(1)(2)(3)的结论计算即可。