题目内容
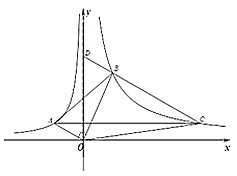
【题目】如图,![]() ,
,![]() ,反比例函数
,反比例函数![]() (
(![]() )过点
)过点![]() ,
,![]() (
(![]() )的图象分别过点
)的图象分别过点![]() 、
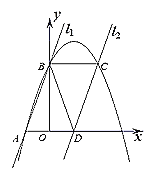
、![]() ,直线BC交y轴于点D,
,直线BC交y轴于点D,![]() ∥
∥![]() 轴.
轴.
(1)求![]() 和
和![]() 的值;
的值;
(2)求![]() 的面积.
的面积.
【答案】(1)1,8;(2)20
【解析】
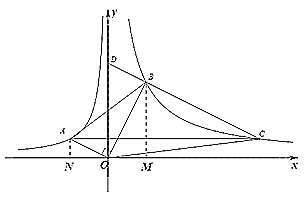
(1)把点A的坐标代入![]() 即可求得a的值,作
即可求得a的值,作![]() ⊥
⊥![]() 轴于
轴于![]() ,作
,作![]() ⊥
⊥![]() 轴于
轴于![]() ,证得
,证得![]() ,根据
,根据![]() ,得到相似比,再利用反比例函数k的几何意义,求得答案;
,得到相似比,再利用反比例函数k的几何意义,求得答案;
(2)先分别求得点C、B的坐标,利用待定系数法求得直线BC的解析式,求得点D的坐标,再用三角形面积公式即可求得答案.
(1)∵点![]() 在
在![]() 上,
上,
∴![]() ,
,![]() ,
,
过点A作![]() ⊥
⊥![]() 轴于
轴于![]() ,作
,作![]() ⊥
⊥![]() 轴于
轴于![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
根据反比例函数![]() 中k值的几何意义知:
中k值的几何意义知:![]() ,
,
故:![]() ,
,![]() ;
;
(2)∵![]() ∥
∥![]() 轴,点C在
轴,点C在![]() 上,
上,
∴点A、C的纵坐标相同,![]() ,
,
∴点C的坐标为:![]() ,
,
由(1)知:![]() ,
,![]()
又![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴点B的坐标为:![]() ,
,
设直线BC的解析式为:![]() ,
,
∴![]() ,
,
解得: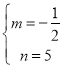 ,
,
∴直线BC的解析式为:![]() ,
,
令![]() ,则
,则![]() ,
,
∴点D的坐标为:![]() ,
,
∴![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目