题目内容
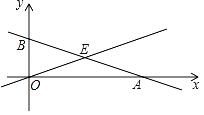
【题目】如图，函数y=﹣
x+2的图象与x轴、y轴分别交于点A、B，与函数y=kx（k为常数）的图象交于点E，以BE、OE为邻边的平行四边形是菱形．
（1）求k；
（2）过点B作y轴的垂线，交函数y=kx的图象于点C，四边形OACB是矩形吗？为什么？
【答案】（1）y=
x（2）是矩形，理由见解析．
【解析】
（1）由题意可得A，B坐标，由BE=OE，可证AE=BE=OE，可求E点坐标，再代入解析式可求k
（2）根据平行线分线段成比例可得OE=EC，可证OACB是平行四边形，且∠AOB=90°可得OACB是矩形
∵函数y=-x+2的图象与x轴、y轴分别交于点A、B
∴A（6，0），B（0，2）
∴BO=2，AO=6
∵OE，BE是菱形的边
∴BE=OE
∴∠ABO=∠BOE
∵∠AOB=90°
∴∠ABO+∠BAO=90°，∠BOE+∠AOE=90°
∴∠BAO=∠AOE
∴OE=AE
∴AE=BE
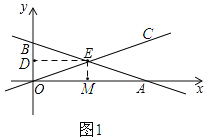
作EM⊥AO，作ED⊥BO
∴EM∥BO，DE∥AO
∴
，
∴ME=1，DE=3
∴E（3，1）
∵y=kx的图象过E点
∴1=3k
∴k=
∴解析式y=x
（2）是矩形．
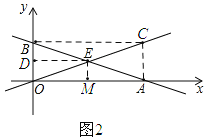
∵BC⊥y轴，AO⊥y轴
∴BC∥AO
∴
∴OE=CE，且AE=BE
∴ACBO是平行四边形且∠AOB=90°
∴四边形ACBO是矩形．
练习册系列答案
相关题目
