题目内容
【题目】如图，已知菱形ABCD，AB=5，对角线BD=8，作AE⊥BC于点E，CF⊥AD于点F，连接EF，求EF的长．
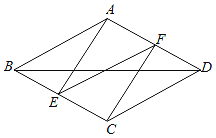
【答案】6.
【解析】试题分析：连接AC交EF于点O，根据菱形的性质通过勾股定理可求出AC的长度，再由AE⊥BC于点E、CF⊥AD于点F，可得出四边形AECF为平行四边形，根据平行四边形的性质，即可得出EF=AC=6，此题得解．
试题解析：
连接AC交EF于点O，如图所示．
∵四边形ABCD为菱形，AB=5、BD=8，
∴AC与BD互相垂直平分，
∴BO=4，AO=
=3，
∴AC=6．
∵AE⊥BC于点E，CF⊥AD于点F，四边形ABCD为菱形，
∴AE∥CF，且AE=CF，
∴四边形AECF为平行四边形，
∴EF=AC=6．
∴EF的长度为6．
练习册系列答案
名师指导一卷通系列答案
相关题目