题目内容
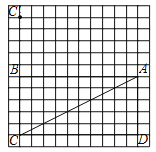
【题目】如图,12×12的正方形网格中的每个小正方形的边长都是1,正方形的顶点叫做格点.矩形ABCD的四个顶点A,B,C,D都在格点上,将△ADC绕点A顺时针方向旋转得到△AD′C′,点C与点C′为对应点.
(1)在正方形网格中确定D′的位置,并画出△AD′C′;
(2)若边AB交边C′D′于点E,求AE的长.
【答案】(1)作图见解析;(2)![]() .
.
【解析】试题分析: ![]() 画图即可.
画图即可.
![]() 根据旋转的性质,可得△ADC≌△AD′C′,设
根据旋转的性质,可得△ADC≌△AD′C′,设![]() 在
在![]() 中,运用勾股定理求解即可.
中,运用勾股定理求解即可.
试题解析:

(2)∵将△ADC绕点A顺时针方向旋转得到△AD′C′,点C与点C′为对应点,
∴△ADC≌△AD′C′,
∴AC=AC′,AD′=AD=5,CD′=CD=10,∠AD′C′=∠ADC=90°,∠AC′D′=∠ACD,
∵AB∥CD,
∴∠BAC=∠ACD,∵AB⊥C C′,AC=AC′,
∴∠BAC=∠C′AB,
∴∠AC′D′=∠C′AB,
∴C′E=AE.
在![]() 中,
中, ![]()
设![]() 则
则![]()
![]() ,
,
解得: ![]()
答:AE的长为: ![]()

练习册系列答案
相关题目