Question

【题目】如图，△ABC中，∠ABC＝60°，AD、CE分别平分∠BAC、∠ACB，AD、CE相交于点P

(1) 求∠CPD的度数

(2) 若AE＝3，CD＝7，求线段AC的长.

Answer 1

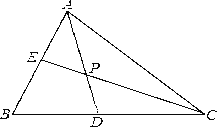
【答案】（1）证明见解析；（2）10.

【解析】试题分析：（1）由题中条件可得△APE≌△APF，进而得出∠APE=∠APF，再利用∠ABC=60°，AD、CE分别平分∠BAC，∠ACB，即可得出答案；

（2）通过角之间的转化可得出△CPF≌△CPD，进而可得出线段之间的关系，即可得出结论．

试题解析：如图，在AC上截取AF=AE，连接PF

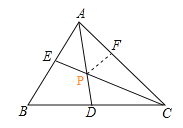
∵AD平分∠BAC，

∴∠BAD=∠CAD，

在△APE和△APF中

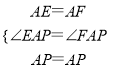
∴△APE≌△APF（SAS），

∴∠AOE=∠APF，

∵∠ABC=60°，AD、CE分别平分∠BAC，∠ACB，

∴∠APC=120°,

∴∠CPD=60°；

（2）∵∠APC=120°，∴∠APE=60°，

∴∠APF=∠CPD=60°=∠CPF，

在△CPF和△CPD中，

,

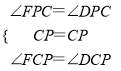∴△CPF≌△CPD（ASA）

∴CF=CD，

∴AC=AF+CF=AE+CD=3+7=10.