题目内容
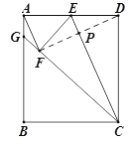
【题目】如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF.
(1)求证:AF∥CE;
(2)探究线段AF,EF,EC之间的数量关系,并说明理由;
(3)若BC=6,BG=8,求AF的长.

【答案】(1)证明见解析;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]()
【解析】(1)由对称的性质可得出相等的边与角,通过等腰三角形的性质及等量代换可得出∠EAF=∠DEC,即可证明AF∥CE;(2)连接DF,证△AFD、△EDC相似,根据相似的性质可推出线段AF,EF,EC之间的数量关系;(3)根据(2)中的数量关系: ![]() ,先求出EC、EF的长,进而可求出AF的长.
,先求出EC、EF的长,进而可求出AF的长.
(1)证明:由折叠矩形ABCD可得,EF=ED,CF=CD
∠DEC=∠FEC,∠EFG=∠EFC=∠EDC=90°
∵点E为AD的中点
∴AE=ED=EF
∴∠EAF=∠EFA
∵∠DEF=∠EAF+∠EFA=∠DEC+∠FEC
∴∠EAF=∠DEC
∴AF∥EC
(2)线段AF,EF,EC之间的数量关系为: ![]() ,理由如下:
,理由如下:
连接DF交EC于P
∵EF=ED, CF=CD
∴E,C两点都在线段DF的中垂线上,即EC⊥DF
∴∠DPE=90°
∵AF∥EC
∴∠AFD=∠DPE=∠EDC=90°
∵∠EAF=∠DEC,∠AFD=∠EDC
∴△AFD∽△EDC
∴![]() ,即
,即![]()
∴![]()
(3)∵∠GAF+∠EAF=∠GFA+∠EFA=90°,∠EAF=∠EFA
∴∠GAF=∠GFA,∴AG=FG
在Rt△BGC中,∵BC=6,BG=8
∴![]()
∵AB=CD=CF,∴8+AG=10-FG,∴AG=FG=1,∴CF=CD=9
∵AD=BC=6,∴![]()
∴在Rt△DEC中, ![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]()

练习册系列答案
相关题目