题目内容
【题目】甲乙两人同时登西山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图像如图所示,根据图像所提供的信息解答下列问题: 
(1)甲登山的速度是每分钟米,乙在A地提速时距地面的高度b为米.
(2)若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,乙追上了甲此时乙距A地的高度为多少米?
【答案】
(1)10;30
(2)解:由图知:x= ![]() +2=11,
+2=11,
∵C(0,100),D(20,300)
∴线段CD的解析式:y甲=10x+100(0≤x≤20);
∵A(2,30),B(11,300),
∴折线OAB的解析式为:y乙= 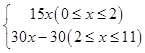
(3)解:由 ![]() ,
,
解得 ![]() ,
,
∴登山6.5分钟时乙追上甲.
此时乙距A地高度为165﹣30=135(米)
【解析】解:(1)甲的速度为:(300﹣100)÷20=10米/分, 根据图中信息知道乙一分的时间,走了15米,
那么2分时,将走30米;(1)甲的速度=(300﹣100)÷20=10,根据图像知道一分的时间,走了15米,然后即可求出A地提速时距地面的高度;(2)乙提速后,乙的速度是甲登山速度的3倍,所以乙的速度是30米/分.那么求出点B的坐标,加上点A的坐标代入一次函数解析式即可求出乙的函数解析式,把C、D坐标代入一次函数解析式可求出甲的函数解析式;(3)乙追上了甲即此时的y的值相等,然后求出时间在计算距A地的高度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



