题目内容
【题目】如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿 D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度变为每秒dcm.图②是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.
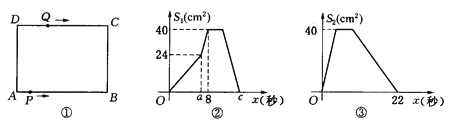
(1)、参照图象,求b、图②中c及d的值;
(2)、连接PQ,当PQ平分矩形ABCD的面积时,运动时间x的值为 ;
(3)、当两点改变速度后,设点P、Q在运动线路上相距的路程为y(cm),求y(cm)与运动时间x(秒)之间的函数关系式,并写出自变量x的取值范围;
(4)、若点P、点Q在运动路线上相距的路程为25cm,求x的值.
【答案】(1)、b=2;C=17;d=1;(2)、![]() ;(3)、当6<x≤
;(3)、当6<x≤![]() 时,y=28-3x 当
时,y=28-3x 当![]() <x≤17时,y=3x-28;当17<x≤22时,y=x+6;(4)、1秒或19秒.
<x≤17时,y=3x-28;当17<x≤22时,y=x+6;(4)、1秒或19秒.
【解析】
试题分析:(1)、首先根三角形面积求出a的值,然后得出b、c、d的值;(2)、平分面积则说明PQ经过四边形对角线的交点;(3)、利用待定系数法分别求出两段函数图像的解析式;(4)、分别根据改变速度前和改变速度后两种情况求出x的值.
试题解析:(1)、观察图②得S△APD=![]() PA
PA![]() AD=
AD=![]() ×a×8=24, ∴a=6(秒),
×a×8=24, ∴a=6(秒),
![]() (厘米/秒),
(厘米/秒), ![]() (秒);
(秒);
(22﹣6)d=28﹣12, 解得d=1(厘米/秒);
(2)、![]()
(3)、当6<x≤![]() 时,y=28-3x 当
时,y=28-3x 当![]() <x≤17时,y=3x-28 当17<x≤22时,y=x+6
<x≤17时,y=3x-28 当17<x≤22时,y=x+6
(4)、改变速度前,28-3x=25,x=1
改变速度后,x+6=25,x=19
∴当点Q出发1或19秒时,点P、点Q在运动路线上相距的路程为25cm.