Question

【题目】如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连接BM、DN．

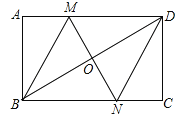
（1）求证：四边形BMDN是菱形；

（2）若AB=4，AD=8，求MD的长。

Answer 1

【答案】（1）证明见解析；（2）MD长为．

【解析】试题分析：（1）根据矩形性质求出AD∥BC，推出∠MDO=∠NBO，∠DMO=∠BNO，证△DMO≌△BNO，推出OM=ON，得出平行四边形BMDN，推出菱形BMDN；

（2）根据菱形性质求出DM=BM，在Rt△AMB中，根据勾股定理得出BM2=AM2+AB2，即可列方程求得．

试题解析：（1）∵四边形ABCD是矩形

∴AD∥BC，∠A=90°，

∴∠MDO=∠NBO，∠DMO=∠BNO，

∵在△DMO和△BNO中

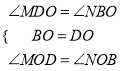
∴△DMO≌△BNO（ASA），

∴OM=ON，

∵OB=OD，

∴四边形BMDN是平行四边形，

∵MN⊥BD，

∴平行四边形BMDN是菱形．

（2）∵四边形BMDN是菱形，

∴MB=MD，

设MD长为x，则MB=DM=x，

在Rt△AMB中，BM2=AM2+AB2

即x2=（4-x）2+22，

解得：x=，

答：MD长为．