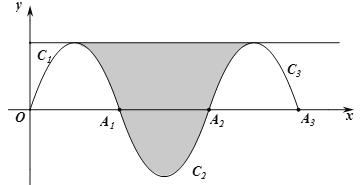
题目内容
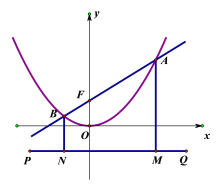
【题目】如图,一段抛物线:![]() ,记为
,记为![]() ,它与
,它与![]() 轴交于两点
轴交于两点![]() ,
,![]() :将
:将![]() 绕
绕![]() 旋转
旋转![]() 得到
得到![]() ,交
,交![]() 轴于
轴于![]() :将
:将![]() 绕
绕![]() 旋转
旋转![]() 得到
得到![]() ,交
,交![]() 轴于
轴于![]() .过抛物线
.过抛物线![]() ,
,![]() 顶点的直线与
顶点的直线与![]() ,
,![]() ,
,![]() 围成的如图中的阴影部分,那么该面积为_________.
围成的如图中的阴影部分,那么该面积为_________.
【答案】![]()
【解析】
先求出点A1、A2、A3的坐标,进一步可求出抛物线C1的顶点F、抛物线C2的顶点H、抛物线C3的顶点G的坐标,由题意可判断F、A1、H三点共线、H、A2、G三点共线,再根据抛物线的对称性可得:S阴影=S△FGH,继而可得结果.
解:对于抛物线C1:![]() ,当y=0时,
,当y=0时,![]() ,所以
,所以![]() ,∴点A1的坐标为(3,0);
,∴点A1的坐标为(3,0);
由题意:将![]() 绕
绕![]() 旋转
旋转![]() 得到
得到![]() ,交
,交![]() 轴于
轴于![]() ,将
,将![]() 绕
绕![]() 旋转
旋转![]() 得到
得到![]() ,交
,交![]() 轴于
轴于![]() ,∴点A2的坐标为(6,0),点A3的坐标为(9,0);
,∴点A2的坐标为(6,0),点A3的坐标为(9,0);
设抛物线C1的顶点为F,抛物线C2的顶点为H,抛物线C3的顶点为G,则F、H、G的坐标分别为(![]() )、(
)、(![]() )、(
)、(![]() ),
),
连接A1F、A1H,如图,根据题意可知F、A1、H三点共线,同理H、A2、G三点共线,
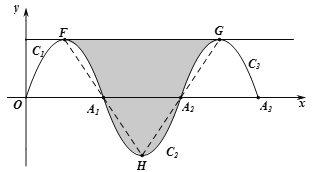
∴由抛物线的对称性可得:S阴影=S△FGH=![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目