题目内容
【题目】如图,D、E分别是AB、AC的中点,CD⊥AB于D,BE⊥AC于E,求证:AC=AB. 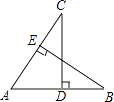
【答案】证明:如图,连接BC 
∵CD⊥AB于D,D是AB的中点,即CD垂直平分AB,
∴AC=BC(中垂线的性质),
∵E为AC中点,BE⊥AC,
∴BC=AB(中垂线的性质),
∴AC=AB.
【解析】作辅助线:连接BC,由CD垂直于AB,且D为AB中点,即CD所在直线为AB的垂直平分线,根据线段垂直平分线上的点到线段两端点的距离相等,得到AC=BC,又E为AC中点,且BE垂直于AC,即BE所在的直线为AC的垂直平分线,同理可得BC=AB,等量代换即可得证.
【考点精析】认真审题,首先需要了解轴对称的性质(关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上).

练习册系列答案
相关题目