��Ŀ����
����Ŀ��(2016�Ĵ�ʡ��ɽ�е�25��)��֪Rt��ABC�У�AB�ǡ�O���ң�б��AC����O�ڵ�D����AD=DC���ӳ�CB����O�ڵ�E��
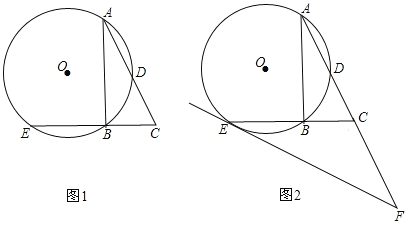
��1��ͼ1��A��B��C��D��E������У��Ƿ����ij�����ľ�������߶�CE�ij�����˵�����ɣ�
��2����ͼ2������E����O�����ߣ���AC���ӳ����ڵ�F��
����CF=CDʱ����sin��CAB��ֵ��
����CF=aCD��a��0��ʱ���Բ���sin��CAB��ֵ�����ú�a�Ĵ���ʽ��ʾ��ֱ��д�������
���𰸡���1��AE=CE����2����![]() ����
����![]() ��
��
��������
�����������1������AE��DE����ͼ1������Բ�ܽǶ����ɵ���ADE=��ABE=90�㣬����AD=DC�����ݴ�ֱƽ���ߵ����ʿɵ�AE=CE��
��2������AE��ED����ͼ2������ABE=90��ɵ�AE����O��ֱ�����������ߵ����ʿɵ���AEF=90�㣬�Ӷ���֤����ADE�ס�AEF��Ȼ���������������ε����ʿɵ�![]() =ADAF������CF=CDʱ���ɵ�
=ADAF������CF=CDʱ���ɵ�![]() ���Ӷ���EC=AE=
���Ӷ���EC=AE=![]() CD����Rt��DEC���������Ǻ����ɵ�sin��CED=
CD����Rt��DEC���������Ǻ����ɵ�sin��CED=![]() ������Բ�ܽǶ����ɵ���CAB=��DEC���������sin��CAB��ֵ������CF=aCD��a��0��ʱ��ͬ�����ɽ�����⣮
������Բ�ܽǶ����ɵ���CAB=��DEC���������sin��CAB��ֵ������CF=aCD��a��0��ʱ��ͬ�����ɽ�����⣮
�����������1��AE=CE�����ɣ�
����AE��DE����ͼ1���ߡ�ABC=90�㣬���ABE=90�����ADE=��ABE=90������AD=DC����AE=CE��
��2������AE��ED����ͼ2���ߡ�ABE=90�㣬��AE����O��ֱ������EF����OO�����ߣ����AEF=90�㣬���ADE=��AEF=90�������ߡ�DAE=��EAF�����ADE�ס�AEF����![]() ����
����![]() =ADAF��
=ADAF��
����CF=CDʱ��AD=DC=CF��AF=3DC����![]() =DC3DC=
=DC3DC=![]() ����AE=
����AE=![]() DC����EC=AE����EC=
DC����EC=AE����EC=![]() DC����sin��CAB=sin��CED=
DC����sin��CAB=sin��CED=![]() =
=![]() =
=![]() ��
��
����CF=aCD��a��0��ʱ��sin��CAB=![]() ��
��
��CF=aCD��AD=DC����AF=AD+DC+CF=��a+2��CD����![]() =DC��a+2��DC=��a+2��
=DC��a+2��DC=��a+2��![]() ����AE=
����AE=![]() DC����EC=AE����EC=
DC����EC=AE����EC=![]() DC����sin��CAB=sin��CED=
DC����sin��CAB=sin��CED=![]() =
=![]() ��
��


