题目内容
【题目】如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′OP=r2 , 则称点P′是点P关于⊙O的“反演点”. 如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
【答案】解:设OA交⊙O于C,连结B′C,如图2, 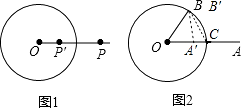
∵OA′OA=42 ,
而r=4,OA=8,
∴OA′=2,
∵OB′OB=42 ,
∴OB′=4,即点B和B′重合,
∵∠BOA=60°,OB=OC,
∴△OBC为等边三角形,
而点A′为OC的中点,
∴B′A′⊥OC,
在Rt△OA′B′中,sin∠A′OB′= ![]() ,
,
∴A′B′=4sin60°=2 ![]() .
.
【解析】设OA交⊙O于C,连结B′C,如图2,根据新定义计算出OA′=2,OB′=4,则点A′为OC的中点,点B和B′重合,再证明△OBC为等边三角形,则B′A′⊥OC,然后在Rt△OA′B′中,利用正弦的定义可求A′B′的长.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
【题目】为了解某校七,八年级学生的睡眠情况,随机抽取了该校七,八年级部分学生进行调查,已知抽取七年级与八年级的学生人数相同,利用抽样所得的数据绘制如下统计图表.
睡眠情况分组表(单位:时)
组别 | 睡眠时间x |
A | x≤7.5 |
B | 7.5≤x≤8.5 |
C | 8.5≤x≤9.5 |
D | 9.5≤x≤10.5 |
E | x≥10.5 |
根据图表提供的信息,回答下列问题:
(1)求统计图中的a;
(2)抽取的样本中,八年级学生睡眠时间在C组的有多少人?
(3)已知该校七年级学生有755人,八年级学生有785人,如果睡眠时间x(时)满足:7.5≤x≤9.5,称睡眠时间合格,试估计该校七、八年级学生中睡眠时间合格的共有多少人?





