题目内容
【题目】如图,△ABC中,点E是BC上的一点,BC=3BE,点D是AC的中点,若S△ADF﹣S△BEF=2.则S△ABC=_____.

【答案】12
【解析】
如图,取AE的中点H,连接DH.首先证明S△AHD=2,求出△AEC,△ABE的面积即可解决问题.
如图,取AE的中点H,连接DH.
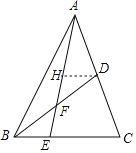
∵AH=HE,AD=DC,
∴DH∥BC,EC=2DH,
∵BC=3BE,
∴EC=2BE,
∴BE=DH,
∵∠HDF=∠EBF,∠HFD=∠EFB,BE=DH,
∴△HDF≌△EBF(AAS),
∴S△EBF=S△HDF,
∵S△ADF﹣S△BEF=2,
∴S△AHD=2,
∵DH∥EC,
∴△AHD∽△AEC,
∴![]() ,
,
∴S△AEC=8,
∵EC=2BE,
∴S△ABE=4,
∴S△ABC=12.

练习册系列答案
相关题目