题目内容
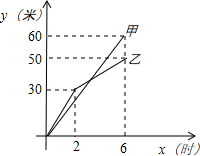有两段长度相等的河渠挖掘任务，分别交给甲乙两个工程队同时进行挖掘，如图是反映所挖河渠长度y（米）与挖掘时间x（时）之间的关系的部分图象．如果甲队施工速度不变，乙队在开挖6小时后，施工速度增加7千米/时，结果两队同时完成了任务，则该河渠的长度为（ ）| A、90米 | B、100米 | C、110米 | D、120米 |
分析：横坐标为施工时间，纵坐标为施工长度，拆线的斜率即为施工速度．在六小时后，解题思路与追赶问题类似．
解答：解：设y1，y2分别为甲，乙施工长度．v1，v2分别为甲，乙施工速度．
设以0h开始记时，施工时间为x小时．
当2＜x＜6时，v1=
=10米/时，v2 =
=5米/时．
当x＞6时，v1=10米/时．v2=5+7=12米/时．
y1=10（x-6）+60=10x
y2=12（x-6）+50=12x-22
当甲乙两队同时完成时，y1=y2
即：10x=12x-22．
解得：x=11．
所以河渠长度为：10×11=110米．
故选：C．
设以0h开始记时，施工时间为x小时．
当2＜x＜6时，v1=
| 60-0 |
| 6-0 |
| 50-30 |
| 6-2 |
当x＞6时，v1=10米/时．v2=5+7=12米/时．
y1=10（x-6）+60=10x
y2=12（x-6）+50=12x-22
当甲乙两队同时完成时，y1=y2
即：10x=12x-22．
解得：x=11．
所以河渠长度为：10×11=110米．
故选：C．
点评：此题为函数图象的应用，解题时根据题设条件找出横纵坐标对应的量的关系，列出解析式再进一步求解．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
14、有两段长度相等的河渠挖掘任务，分别交给甲、乙两个工程队同时进行挖掘．下图是反映所挖河渠长度y（米）与挖掘时间x（时）之间关系的部分图象．开挖
同时完成了任务．问甲队从开挖到完工所挖河渠的长度为多少米？
长度y（米）与挖掘时间x（时）之间关系的部分图象．请解答下列问题：