题目内容
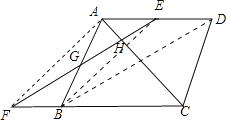
【题目】如图，菱形ABCD中，E是AD的中点，EF⊥AC交CB的延长线于点F．
（1）DE和BF相等吗？请说明理由．
（2）连接AF、BE，四边形AFBE是平行四边形吗？说明理由．
【答案】
【1】(1)相等，连接BD，证明四边形DEFB是平行四边形，则BF=DE=AE
【2】(2)是平行四边形，理由是AE平行且等于BF
【解析】试题分析：（1）、连接BD，AF，BE，根据菱形的性质得出AC⊥BD，结合EF⊥AC得出EF∥BD，结合ED∥FB得出四边形EDBF是平行四边形，从而得出结论；（2）、根据E为AD的中点得出AE=ED，则AE=BF，结合AE∥BF得出四边形AEBF为平行四边形，从而说明结论.
试题解析：（1）、连接BD，AF，BE， 在菱形ABCD中，AC⊥BD ∵EF⊥AC，
∴EF∥BD，又ED∥FB， ∴四边形EDBF是平行四边形，DE=BF，
（2）、∵E为AD的中点， ∴AE=ED，∴AE=BF， 又AE∥BF， ∴四边形AEBF为平行四边形，
即AB与EF互相平分．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
【题目】有这样一个问题：探究函数
的图象与性质.小华根据学习函数的经验，对函数的图象与性质进行了探究.下面是小华的探究过程，请补充完整：
（1）在函数中，自变量x的取值范围是________．
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 5 | 4 | 3 | 2 | 1 | 0 | 1 | 2 | m | … |
①求m的值；
②在平面直角坐标系xOy中，描出以上表中各组对应值为坐标的点，并根据描出的点，画出该函数的图象．
（2）结合函数图象写出该函数的一条性质：________．
