题目内容
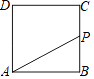
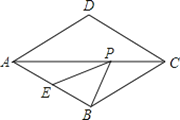
【题目】如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( ).
A. 1 B. 2 C. ![]() D.
D. ![]()
【答案】D
【解析】根据轴对称最短问题作法首先求出P点的位置,再结合菱形的性质得出△AEE′为等边三角形,进而求出PE+PB的最小值.
解:如图所示,
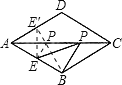
作E点关于AC对称点E′点,连接E′B,E′B与AC的交点即是P点,
∵菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,
∴AE′=AE=BE=1,∴△AEE′为等边三角形,∴∠AEE′=60°,
∴∠E′EB=120°,
∵BE=EE′,∴∠EE′B=30°,∴∠AE′B=90°,
BE′=![]() ,∵PE+PB=BE′,
,∵PE+PB=BE′,
∴PE+PB的最小值是: ![]() .
.
故答案为: ![]() .
.
“点睛”此题主要考查了菱形的性质以及轴对称中最短路径求法,正确地作出P点从而利用菱形性质得出是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目