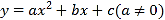题目内容
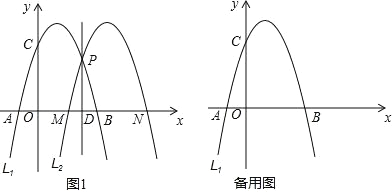
【题目】如图 1,已知抛物线 L1:y=﹣x2+2x+3 与 x 轴交于 A,B 两点(点 A在点 B 的左侧),与 y 轴交于点 C,在 L1 上任取一点 P,过点 P 作直线 l⊥x 轴, 垂足为D,将 L1 沿直线 l 翻折得到抛物线L2,交 x 轴于点 M,N(点 M 在点 N 的左侧).
(1)当 L1 与 L2 重合时,求点 P 的坐标;
(2)当点 P 与点 B 重合时,求此时 L2 的解析式;并直接写出 L1 与 L2 中,y 均随x 的增大而减小时的 x 的取值范围;
(3)连接 PM,PB,设点 P(m,n),当 n=![]() m 时,求△PMB 的面积.
m 时,求△PMB 的面积.
【答案】(1) P(1,4);(2) y=﹣x2+10x﹣21;x≥5 ;(3) ![]() 或 3.
或 3.
【解析】
(1)当点 P 为抛物线 L1 的顶点时,抛物线 L1 与 L2 重合,把y=﹣x2+2x+3变形为顶点式即可得P点坐标;(2)令 y=0,可求出P点坐标,可知L1 与 L2的对称轴,进而可得L2的顶点坐标,即可求出L2的解析式;根据图像可得L1 与 L2 中,y 均随x 的增大而减小时的 x 的取值范围;(3)把P(m,![]() )代入L1解析式可求出m的值
)代入L1解析式可求出m的值
,根据三角形面积公式求出S△PNB的值即可.
(1)由抛物线对称性,当点 P 为抛物线 L1 的顶点时,抛物线 L1 与 L2 重合
∵y=﹣x2+2x+3=﹣(x﹣1)2+4
∴点 P(1,4);
(2)在抛物线 L1 中,令 y=0,即﹣x2+2x+3=0
解得 x1=﹣1,x2=3
当点 P 与点 B 重合时,此时 P(3,0)
∴抛物线 L2 与抛物线 L1 关于直线 x=3 对称
∴抛物线 L2 的顶点为(5,4)
∵由抛物线对称性可知,抛物线 L1 和 L2 开口方向和大小相同.
∴抛物线 L2 和的解析式为 y=﹣(x﹣5)2+4=﹣x2+10x﹣21
∴结合图象可知,当 x≥5 时,抛物线 L1 与抛物线L2 中,y 均随 x 的增大而减小
(3)当 n=![]() 时,﹣m2+2m+3=
时,﹣m2+2m+3=![]() ,
,
解得 m1=﹣![]() ,m2=2,
,m2=2,
∴点 P 坐标为(﹣![]() ,﹣
,﹣![]() )或(2,3)
)或(2,3)
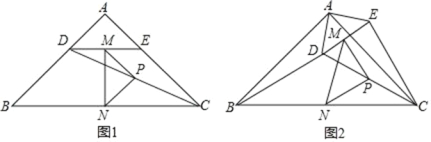
①如图1,
当点 P 坐标为(﹣![]() ,﹣
,﹣![]() )时,点 D 的坐标为坐标为(﹣
)时,点 D 的坐标为坐标为(﹣![]() ,0)
,0)
∴DB=3﹣(﹣![]() )=
)=![]()
∴MB=2BD=2×![]() =9
=9
∴S△PMB=![]() =
=![]()
②如图 2,
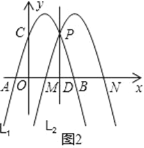
当点 P 坐标为(2,3)时,点 D 的坐标为坐标为(2,0)
∴DB=3﹣2=1
∴MB=2BD=2
∴S△PMB=![]() =3
=3
综上所述:当点P(m,n),n=![]() 时,△PMB 的面积为
时,△PMB 的面积为![]() 或 3.
或 3.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案