��Ŀ����
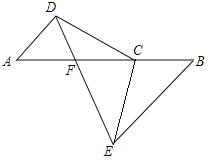
����Ŀ����ͼ��MΪ������ABD�ĵ�AB���е㣬��D��DC��AB������BC��AB=8cm��DM=4cm��DC=1cm������P��A���������AB�������˶�������Q�Ե�B������������BC��CD�������˶����ٶȾ�Ϊ1cm/s��������һ�����㵽���յ�ʱ������ͬʱֹͣ�˶������P�˶�t��s��ʱ����MPQ�����ΪS�����ܹ��ɡ�MPQ�Ķ�����⣩��
��1��t��s��Ϊ��ֵʱ����Q��BC���˶���t��s��Ϊ��ֵʱ����Q��CD���˶���
��2����S��t֮��ĺ�����ϵʽ��
��3����tΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
��4������Q��CD���˶�ʱ��ֱ��д��tΪ��ֵʱ����MPQ�ǵ��������Σ�
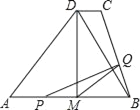
���𰸡���1����0��t��5��t��4��s��ʱ����Q��BC���˶�����5��t��6��s��ʱ����Q��CD���˶�����2����0��t��4ʱS=��![]() t2+
t2+![]() ����4��t��5ʱ��S=
����4��t��5ʱ��S=![]() t2��
t2��![]() ����5��t��6ʱ��S=2t��8����3����t=6ʱ��Sȡ�����ֵ�����ֵΪ4����4����t=
����5��t��6ʱ��S=2t��8����3����t=6ʱ��Sȡ�����ֵ�����ֵΪ4����4����t=![]() ��ʱ����MPQ�ǵ��������Σ�
��ʱ����MPQ�ǵ��������Σ�
�������������������1������C��CE��AB������ΪE������֤���ı���DCEM�Ǿ��Σ��Ӷ��������![]() �ij���Ȼ���Dz��ܹ���
�ij���Ȼ���Dz��ܹ���![]() ����������ɽ�����⣮
����������ɽ�����⣮
��2�����ڵ�P�ڵ�M������ʱPM�ı���ʽ��ͬ����Q���߶�BC��DC��ʱ��Q��PM�ľ���ı���ʽ��ͬ������������������ۣ���ͼ1��2��3��ʾ��Ȼ��ֻ����t�Ĵ���ʽ��ʾ��PM������ϵĸߣ��Ϳ����S��t֮��ĺ�����ϵʽ��
��3�����ö��κ�����һ�κ��������ʶԣ�2���е�����������з��������ɽ�����⣮
��4����֤QM��MP��QP��MP.��![]() �ǵ��������Σ�ֻ����
�ǵ��������Σ�ֻ����![]() ��
��![]() �ɵã�
�ɵã� ![]() ����
����![]() �ɵõ�����t�ķ��̣���������̼��ɽ�����⣮
�ɵõ�����t�ķ��̣���������̼��ɽ�����⣮
���������(1)����C��CE��AB������ΪE����ͼ1��
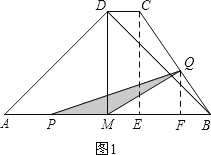
��DA=DB��AM=BM��
��DM��AB.
��CE��AB��
��![]()
��CE��DM.
��DC��ME,CE��DM, ![]()
���ı���DCEM�Ǿ��Σ�
��CE=DM=4��ME=DC=1.
��AM=BM,AB=8,
��AM=BM=4.
��BE=BMME=3.
��![]()
��CB=5.
�ߵ�t=4ʱ����P���M�غϣ����ܹ��ɡ�MPQ��
��t��4.
�൱![]() ��t��4(s)ʱ,��Q��BC���˶�;��
��t��4(s)ʱ,��Q��BC���˶�;��![]() (s)ʱ����Q��CD���˶�.
(s)ʱ����Q��CD���˶�.
(2)�ٵ�0<t<4ʱ����P���߶�AM�ϣ���Q���߶�BC�ϣ�
����Q��QF��AB������ΪF����ͼ1��
��QF��AB��CE��AB��
��![]()
��QF��CE.
���QFB�ס�CEB.
��![]()
��CE=4��BC=5��BQ=t��
��![]()
��![]()
��PM=AMAP=4t��
��![]()
�ڵ�![]() ʱ����P���߶�BM�ϣ���Q���߶�BC�ϣ�
ʱ����P���߶�BM�ϣ���Q���߶�BC�ϣ�
����Q��QF��AB������ΪF����ͼ2��
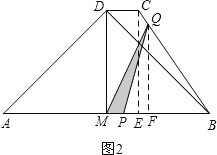
��QF��AB,CE��AB,
��![]()
��QF��CE.
���QFB�ס�CEB.
��![]()
��CE=4��BC=5��BQ=t��
��![]()
��![]()
��PM=APAM=t4��
��![]()
�۵�![]() ʱ����P���߶�BM�ϣ���Q���߶�DC�ϣ�
ʱ����P���߶�BM�ϣ���Q���߶�DC�ϣ�
����Q��QF��AB������ΪF����ͼ3��
��ʱQF=DM=4.
��PM=APAM=t4��
��![]()
������������![]() ��
��![]() ʱ,
ʱ, ![]() ��
��![]() ʱ��S=2t8.
ʱ��S=2t8.
(3)�ٵ�0<t<4ʱ, ![]()
��![]() 0<2<4��
0<2<4��
�൱t=2ʱ,Sȡ�����ֵ,���ֵΪ![]()
�ڵ�![]() ʱ,
ʱ, ![]() �Գ���Ϊx=2.
�Գ���Ϊx=2.
��![]()
�൱x>2ʱ��S����t�����������
�൱t=5ʱ,Sȡ�����ֵ,���ֵΪ![]()
�۵�![]() ʱ��S=2t8.
ʱ��S=2t8.
��2>0��
��S����t�����������,
�൱t=6ʱ��Sȡ�����ֵ�����ֵΪ2��68=4.
������������t=6ʱ��Sȡ�����ֵ�����ֵΪ4.
(4)����Q��CD���˶���![]() ʱ����ͼ3��
ʱ����ͼ3��
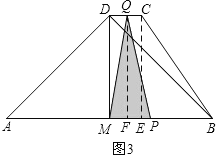
����![]()
![]() ����
����![]()
��MP=t4<64����MP<2��
��QM��MP��QP��MP.
����MPQ�ǵ��������Σ���QM=QP.
��QM=QP��QF��MP��
��MF=PF=12MP.
��MF=DQ=5+1t=6t��MP=t4��
��![]()
��ã� ![]()
�൱t=![]() ��ʱ����MPQ�ǵ���������.
��ʱ����MPQ�ǵ���������.

 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д� ��ѧ�����ϵ�д�
��ѧ�����ϵ�д�����Ŀ��ij�̳�����Ƹһ��Ա�������мס������˾�Ƹ��ͨ������������Ժ���Ʒ֪ʶ������ԣ����Ǹ��Գɼ����ٷ��ƣ����±���ʾ��
Ӧ���� | ����� | ���� | ��Ʒ֪ʶ |
�� | 70 | 50 | 80 |
�� | 60 | 60 | 80 |
��1�����̳���Ҫ��Ƹ������Ʒ��װ�ϼܵ���Ա���Լ���������Ժ���Ʒ֪ʶ�ֱ�Ȩ2��3��5����������Ӧ���ߵ�ƽ���ɼ����ӳɼ�����Ӧ��¼ȡ˭��
��2�����̳���Ҫ��Ƹ��������Ա������������Ժ���Ʒ֪ʶ�ɼ��ֱ�ռ50%��30%��20%����������Ӧ���ߵ�ƽ���ɼ����ӳɼ�����Ӧ��¼ȡ˭��
����Ŀ��ij���������������ij��˾��Ʊ1000�ɣ�ÿ��27Ԫ���±�Ϊ������ÿ�ոù�Ʊ���ǵ��������λ��Ԫ�����������������̣�
���� | һ | �� | �� | �� | �� |
ÿ�� �ǵ� | +4 | +4.5 | ��1 | ��1.5 | ��4 |
��1������������ʱ��ÿ���Ƕ���Ԫ��
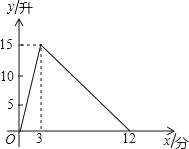
��2�������������ÿ�ɶ���Ԫ����ͼ���ÿ�ɶ���Ԫ��
��3����֪�ù��������Ʊʱ����0.15%�������ѣ�����ʱ�踶�ɽ���0.15%�������Ѻ�0.1%�Ľ���˰�����ù���������������ǰ��ȫ����Ʊ�������������������Σ�