题目内容
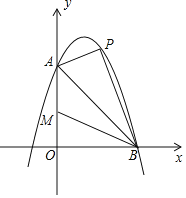
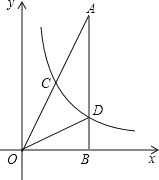
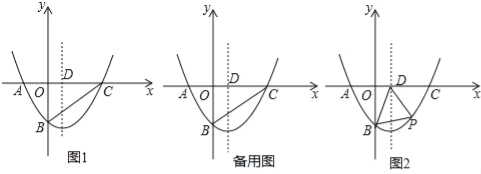
【题目】如图，在平面直角坐标系xOy中，二次函数y=ax2+bx﹣4（a≠0）的图象与x轴交于A（﹣2，0）、C（8，0）两点，与y轴交于点B，其对称轴与x轴交于点D．
（1）求该二次函数的解析式；
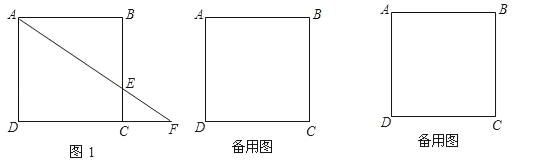
（2）如图1，连结BC，在线段BC上是否存在点E，使得△CDE为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由；
（3）如图2，若点P（m，n）是该二次函数图象上的一个动点（其中m＞0，n＜0），连结PB，PD，BD，求△BDP面积的最大值及此时点P的坐标．
【答案】（1）y=
x2﹣
x﹣4；（2）（8﹣2
，﹣
）、（0，﹣4）、（
，﹣
）；（3）（
，﹣
）．
【解析】
试题分析：（1）∵二次函数y=ax2+bx﹣4（a≠0）的图象与x轴交于A（﹣2，0）、C（8，0）两点，∴
，解得
，∴该二次函数的解析式为y=x2﹣x﹣4；
（2）由二次函数y=
x2﹣x﹣4可知对称轴x=3，∴D（3，0），∵C（8，0），∴CD=5，由二次函数y=x2﹣x﹣4可知B（0，﹣4），设直线BC的解析式为y=kx+b，∴
，解得
，∴直线BC的解析式为y=
x﹣4，设E（m， m﹣4），当DC=CE时，EC2=（m﹣8）2+（m﹣4）2=CD2，即（m﹣8）2+（m﹣4）2=52，解得m1=8﹣2
，m2=8+2（舍去），∴E（8﹣2，﹣）；当DC=DE时，ED2=（m﹣3）2+（
m﹣4）2=CD2，即（m﹣3）2+（m﹣4）2=52，解得m3=0，m4=8（舍去），∴E（0，﹣4）；当EC=DE时，（m﹣8）2+（m﹣4）2=（m﹣3）2+（m﹣4）2解得m5=5.5，∴E（
，﹣
）．综上，存在点E，使得△CDE为等腰三角形，所有符合条件的点E的坐标为（8﹣2，﹣）、（0，﹣4）、（，﹣）．
（3）过点P作y轴的平行线交x轴于点F，∵P点的横坐标为m，∴P点的纵坐标为
m2﹣
m﹣4，∵△PBD的面积S=S梯形﹣S△BOD﹣S△PFD=
m[4﹣（m2﹣m﹣4）]﹣
（m﹣3）[﹣（
m2﹣
m﹣4）]﹣×3×4=﹣
m2+
m=﹣（m﹣）2+
，∴当m=时，△PBD的最大面积为，∴点P的坐标为（，﹣）．
