Question

【题目】如图，在△ABC中，AB＝AC＝4，P为BC边上任意一点．

(1)求证：AP2＋PB·PC＝16.

(2)若BC边上有100个不同的点(不与点B，C重合)P1，P2，…，P100，设mi＝APi2＋PiB·PiC(i＝1，2，…，100)．求m1＋m2＋…＋m100的值．

Answer 1

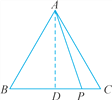
【答案】(1)16;(2)1600

【解析】试题分析：（1）作AD⊥BC于D，由等腰三角形的三线合一性质和勾股定理得出AP2+BPPC=AB2即可；
（2）根据勾股定理，得APi2=AD2+DPi2=AD2+（BD-BPi）2=AD2+BD2-2BDBPi+BPi2，PiBPiC=PiB（BC-PiB）=2BDBPi-BPi2，从而求得mi=AD2+BD2，即可求解．

试题解析：

(1)过点A作AD⊥BC于点D.

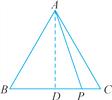
∵AB＝AC，AD⊥BC，

∴BD＝CD，∠ADB＝∠ADC＝90°，

∴AP2＋PB·PC＝AP2＋(PD＋BD)(CD－PD)＝AP2＋CD2－PD2.

∵AP2－PD2＝AD2，

∴AP2＋PB·PC＝AD2＋CD2＝AC2＝16.

(2)由(1)知mi＝APi2＋PiB·PiC＝16，

∴m1＝m2＝…＝m100＝16，

∴m1＋m2＋…＋m100＝16×100＝1600.