题目内容
如图，MN是⊙O的直径，若∠E=25°，∠PMQ=35°，则∠MQP=（ ）| A、30° | B、35° | C、40° | D、50° |
分析：连接PO、QO，根据圆周角定理，得∠POQ=2∠PMQ=70°，则∠OPQ=∠OQP=55°，则∠POM=80°，再根据圆周角定理即可求解．
解答：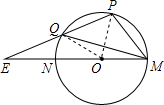
解：连接PO、QO．
根据圆周角定理，得
∠POQ=2∠PMQ=70°，
又OP=OQ，
则∠OPQ=∠OQP=55°，
则∠POM=∠E+∠OPE=80°，
所以∠PQM=
∠POM=40°．
故选C．
解：连接PO、QO．根据圆周角定理，得
∠POQ=2∠PMQ=70°，
又OP=OQ，
则∠OPQ=∠OQP=55°，
则∠POM=∠E+∠OPE=80°，
所以∠PQM=
| 1 |
| 2 |
故选C．
点评：此题综合运用了圆周角定理、等边对等角、三角形的外角的性质．
练习册系列答案
相关题目
