题目内容
【题目】(本题4分+5分=9分)
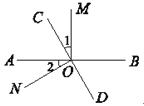
如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,求∠NOC的度数;(2)若∠1=![]() ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.
【答案】(1)90°;(2)150°
【解析】试题分析:(1)由垂线的性质求得∠AOM=∠BOM=90°,然后根据等量代换及补角的定义解答;
(2)根据垂线的定义求得∠AOM=∠BOM=90°,再由∠1=![]() ∠BOC求得∠BOC=120°;然后根据对顶角的性质及补角的定义解答即可.
∠BOC求得∠BOC=120°;然后根据对顶角的性质及补角的定义解答即可.
试题解析:(1)∵OM⊥AB,∠1=∠2,
∴∠1+∠AOC=∠2+∠AOC=90°,即∠CON=90°;
又∠NOC+∠NOD=180°,
∴∠NOD=90°;
(2)∵OM⊥AB,∠1=![]() ∠BOC,
∠BOC,
∴∠BOC=120°,∠1=30°;
又∠AOC+∠BOC=180°,
∴∠AOC=60°;
而∠AOC=∠BOD(对顶角相等),
∴∠MOD=∠MOB+∠AOC=150°

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
【题目】已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.
![]()
水银柱的长度x(cm) | 4.2 | … | 8.2 | 9.8 |
体温计的读数y(℃) | 35.0 | … | 40.0 | 42.0 |
(1)求y关于x的函数关系式(不需要写出函数的定义域);
(2)用该体温计测体温时,水银柱的长度为6.2cm,求此时体温计的读数.