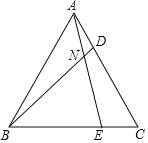
题目内容
【题目】如图,点C在线段AB上,△DAC和△DBE都是等边三角形. 
(1)求证:△DAB≌△DCE;
(2)求证:DA∥EC.
【答案】
(1)证明:∵△DAC和△DBE都是等边三角形,
∴DA=DC,DB=DE,∠ADC=∠BDE=60°,
∴∠ADC+∠CDB=∠BDE+∠CDB,即∠ADB=∠CDE,
在△DAB和△DCE中,
 ,
,
∴△DAB≌△DCE(SAS)
(2)证明:∵△DAB≌△DCE,
∴∠A=∠DCE=60°,
∵∠ADC=60°,
∴∠DCE=∠ADC,
∴DA∥EC
【解析】(1)由△DAC和△DBE都是等边三角形,利用等边三角形的性质得到两对边相等,两个角为60度,利用等式的性质得到夹角相等,利用SAS即可得证;(2)由全等三角形的对应角相等得到∠A=∠DCE=60°,再由∠ADC=60°,得到一对内错角相等,利用内错角相等两直线平行即可得证.
【考点精析】掌握等边三角形的性质是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
【题目】某校课外兴趣小组在本校学生中开展“感动中国2014年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |

(1)表中的a=________,b=________;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?