题目内容
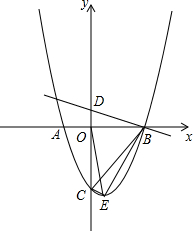 已知抛物线y=ax2-2x+c与x轴交于A(-1,0)、B两点,与y轴交于点C,对称轴为x=1,顶点为E,直线y=-
已知抛物线y=ax2-2x+c与x轴交于A(-1,0)、B两点,与y轴交于点C,对称轴为x=1,顶点为E,直线y=-| 1 | 3 |
(1)求抛物线的解析式;
(2)求证:△BCE∽△BOD;
(3)点P是抛物线上的一个动点,当点P运动到什么位置时,△BDP的面积等于△BOE的面积?
分析:(1)在抛物线y=ax2-2x+c中,已知对称轴x=-
=1,可求出a的值;再将点A的坐标代入抛物线的解析式中,可确定c的值,由此得解.
(2)首先由抛物线的解析式,确定点B、C、E的坐标,由直线BD的解析式能得到点D的坐标;在求出△BCE、△BOD的三边长后,由SSS来判定这两个三角形相似.
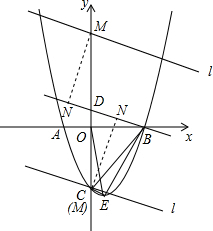
(3)△BOE的面积易得,而在(2)中求出了BD的长,由△BDP、△BOE的面积相等先求出点P到直线BD的距离,如何由这个距离求出点P的坐标?这里需要进行适当的转化;首先在y轴上取一点(可设为点M),使得点M到直线BD的距离等于点P到直线BD的距离,通过解直角三角形先求出DM的长,由此确定点M的坐标,然后过M作平行于直线BD的直线,再联立抛物线的解析式即可确定点P的坐标.
| b |
| 2a |
(2)首先由抛物线的解析式,确定点B、C、E的坐标,由直线BD的解析式能得到点D的坐标;在求出△BCE、△BOD的三边长后,由SSS来判定这两个三角形相似.
(3)△BOE的面积易得,而在(2)中求出了BD的长,由△BDP、△BOE的面积相等先求出点P到直线BD的距离,如何由这个距离求出点P的坐标?这里需要进行适当的转化;首先在y轴上取一点(可设为点M),使得点M到直线BD的距离等于点P到直线BD的距离,通过解直角三角形先求出DM的长,由此确定点M的坐标,然后过M作平行于直线BD的直线,再联立抛物线的解析式即可确定点P的坐标.
解答:解:(1)抛物线y=ax2-2x+c中,对称轴x=-
=-
=1,∴a=1;
将点A(-1,0)代入y=ax2-2x+c中,得:1+2+c=0,c=-3;
∴抛物线的解析式:y=x2-2x-3.
(2)∵抛物线的解析式:y=x2-2x-3=(x-1)2-4=(x+1)(x-3),
∴点C(0,-3)、B(3,0)、E(1,-4);
易知点D(0,1),则有:
OD=1、OB=3、BD=
;
CE=
、BC=3
、BE=2
;
∴
=
=
;
∴△BCE∽△BOD.
 (3)S△BOE=
(3)S△BOE=
×BO×|yE|=
×3×4=6;
∴S△BDP=
×BD×h=S△BOE=6,即 h=
.
在y轴上取点M,过点M作MN⊥BD于N,使得MN=h=
;
在Rt△MND中,sin∠MDB=
,且 MN=
;则 MD=
=4;
∴点M(0,-3)或(0,5).
过点M作直线l∥MN,如右图,则 直线l:y=-
x-3或y=-
x+5,联立抛物线的解析式有:
或
解得:
、
、
、
∴当点P的坐标为(0,-3)、(
,-
)、(
,
)、(
,
)时,△BDP的面积等于△BOE的面积.
| b |
| 2a |
| -2 |
| 2a |
将点A(-1,0)代入y=ax2-2x+c中,得:1+2+c=0,c=-3;
∴抛物线的解析式:y=x2-2x-3.
(2)∵抛物线的解析式:y=x2-2x-3=(x-1)2-4=(x+1)(x-3),
∴点C(0,-3)、B(3,0)、E(1,-4);
易知点D(0,1),则有:
OD=1、OB=3、BD=
| 10 |
CE=
| 2 |
| 2 |
| 5 |
∴
| OD |
| CE |
| OB |
| BC |
| BD |
| BE |
∴△BCE∽△BOD.
 (3)S△BOE=
(3)S△BOE=| 1 |
| 2 |
| 1 |
| 2 |
∴S△BDP=
| 1 |
| 2 |
| 12 | ||
|
在y轴上取点M,过点M作MN⊥BD于N,使得MN=h=
| 12 | ||
|
在Rt△MND中,sin∠MDB=
| 3 | ||
|
| 12 | ||
|
| MN |
| sin∠MDB |
∴点M(0,-3)或(0,5).
过点M作直线l∥MN,如右图,则 直线l:y=-
| 1 |
| 3 |
| 1 |
| 3 |
|
|
解得:
|
|
|
|
∴当点P的坐标为(0,-3)、(
| 5 |
| 3 |
| 32 |
| 9 |
5+
| ||
| 6 |
85-
| ||
| 18 |
5-
| ||
| 6 |
85+
| ||
| 18 |
点评:该题涉及到抛物线解析式的确定、相似三角形的判定和性质以及图形面积的解法等重点知识;最后一题中,由于BD不与x轴、y轴垂直,给解答带来了难度,但通过将BD边上的高进行适当转化,得出过点P且与BD平行的直线l的解析式是突破题目的关键.

练习册系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=