题目内容
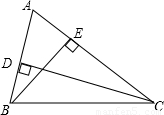
如图，锐角三角形ABC中，CD，BE分别是AB，AC边上的高，垂足为D，E．（1）证明：△ACD∽△ABE．
（2）若将D，E连接起来，则△AED与△ABC能相似吗？说说你的理由．
【答案】分析：（1）根据已知利用有两个角相等的三角形相似判定即可；
（2）根据第一问可得到AD：AE=AC：AB，有一组公共角∠A，则可根据两组对应边的比相等且相应的夹角相等的两个三角形相似进行判定．
解答：证明：（1）∵CD，BE分别是AB，AC边上的高，
∴∠ADC=∠AEB=90°．
∵∠A=∠A，
∴△ACD∽△ABE．
（2）∵△ACD∽△ABE，
∴AD：AE=AC：AB．
∵∠A=∠A，
∴△AED∽△ABC．
点评：此题主要考查学生对相似三角形的判定方法的理解及运用．
（2）根据第一问可得到AD：AE=AC：AB，有一组公共角∠A，则可根据两组对应边的比相等且相应的夹角相等的两个三角形相似进行判定．
解答：证明：（1）∵CD，BE分别是AB，AC边上的高，
∴∠ADC=∠AEB=90°．
∵∠A=∠A，
∴△ACD∽△ABE．
（2）∵△ACD∽△ABE，
∴AD：AE=AC：AB．
∵∠A=∠A，
∴△AED∽△ABC．
点评：此题主要考查学生对相似三角形的判定方法的理解及运用．
练习册系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
16、如图，锐角三角形ABC的边AB，AC上的高线CE和BF相交于点D，请写出图中的两对相似三角形：
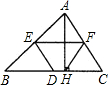如图，锐角三角形ABC中（AB＞AC），AH⊥BC，垂足为H，E、D、F分别是各边的中点，则四边形EDHF是（ ）| A、梯形 | B、等腰梯形 | C、直角梯形 | D、矩形 |
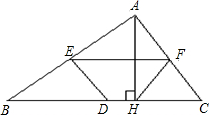如图，锐角三角形ABC中，（AB＞AC），AH⊥BC，垂足为H，E、D、F分别是各边的中点，求证：四边形EDHF是等腰梯形．
28、如图，锐角三角形ABC中，BC＞AB＞AC，小靖依下列方法作图：
如图，锐角三角形ABC中，AD⊥BC，BE⊥AC，垂足分别为D和E，AP∥BC且与BE的延长线交于点P，又边AB、AC的长是关于x的一元二次方程x2-x+