题目内容
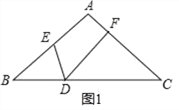
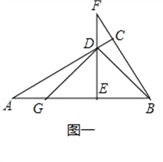
【题目】如图一,∠ACB=90°,点D在AC上,DE⊥AB垂足为E,交BC的延长线于F,DE=EB,EG=EB,
(1)求证:AG=DF;
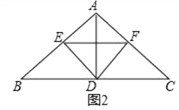
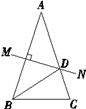
(2)过点G作GH⊥AD,垂足为H,与DE的延长线交于点M,如图二,找出图中与AB相等的线段,并证明.

【答案】(1)证明见解析; (2)AB=DM,证明见解析.
【解析】分析:(1)根据已知条件得到DE=EB=EB,∠EGD=∠EGD=∠EDB=∠EBD=45°,进而证得∠AGD=∠FDB=135°,根据三角形内角和证得∠A=∠F,由三角形外角定理证得∠ADG=∠FBD,根据三角形的判定证得△ADG≌△FDB,由全等三角形的判定即可证得结论;
(2)根据已知条件得到△AED≌△FEB,由全等三角形的性质得到AE=EM,即可得到结论.
本题解析:(1)∵DE=EB,EG=EB,DE⊥AB,
∴DE=EB=EG,
∴∠EGD=∠EDG=∠EDB=∠EBD=45°,
∴∠AGD=∠FDB=135°,
∵∠ACB=90°,∠AED=90°,∠ADE=∠FDC,
∴∠A=∠F,
∴∠ADG=∠FBD,
在△ADG和△FDB中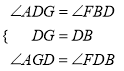
∴△ADG≌△FDB,
∴AG=DF;
(2)∵DE=EB,EG=EB,
∴DE=EB=EG,∵DE⊥AB,
在△AED和△FEB中, 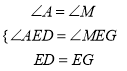
∴△AED≌△MEB,
∴AE=EM,
∴AE+EB=EM+DE,
即AB=DM.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目