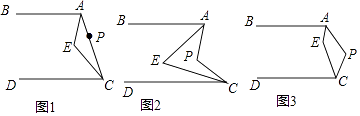
题目内容
【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形B,C,E在同一条直线上,连结DC. 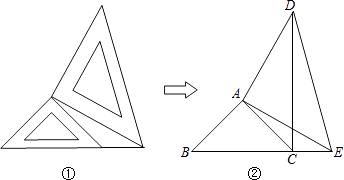
(1)请找出图②中的全等三角形,并给予说明(注意:结论中不得含有未标识的字母);
(2)请判断DC与BE的位置关系,并证明;
(3)若CE=2,BC=4,求△DCE的面积.
【答案】
(1)解:△ABE≌△ACD,
∵△ABC和△ADE是等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°,
∴∠BAC+∠EAC=∠DAE+∠EAC,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
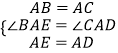
∴△ABE≌△ACD(SAS)
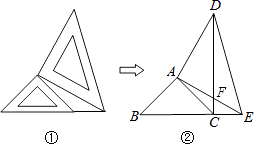
(2)解:∵△ABE≌△ACD,
∴∠AEB=∠ADC.
∵∠ADC+∠AFD=90°,
∴∠AEB+∠AFD=90°.
∵∠AFD=∠CFE,
∴∠AEB+∠CFE=90°,
∴∠FCE=90°,
∴DC⊥BE
(3)解:∵CE=2,BC=4,
∴BE=6,
∵△ABE≌△ACD,
∴CD=BE=6,
∴△DCE的面积= ![]() CECD=
CECD= ![]() ×2×6=6
×2×6=6
【解析】(1)根据等腰直角三角形的性质可以得出△ABE≌△ACD;(2)由△ABE≌△ACD可以得出∠AEB=∠ADC,进而得出∠AEC=90°,就可以得出结论;(3)根据三角形的面积公式即可得到结论.
【考点精析】关于本题考查的等腰直角三角形,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能得出正确答案.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目