题目内容
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,∠ABC=∠ADE=90° ,CD与BE、AE分别交于点P、M.
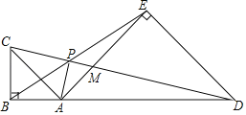
求证:(1)△BAE∽△CAD;
(2)2CB2=CPCM.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由相似三角形定理证明即可.
(2)先证明△CAP∽△CMA,即可得AC2=CPCM,由此可得2CB2=CPCM.
(1)证明:由已知:AC=![]() AB,AD=
AB,AD=![]() AE
AE
∴![]()
∵∠BAC=∠EAD
∴∠BAE=∠CAD
∴△BAE∽△CAD
(2)由(1)得到![]() ,
,
∵△BAE∽△CAD
∴∠BEA=∠CDA
∵∠PME=∠AMD
∴△PME∽△AMD
∴![]() ,
,
∴MPMD=MAME
∠PMA=∠DME
∴△PMA∽△EMD
∴∠APD=∠AED=90°
∵∠CAE=180°∠BAC∠EAD=90°
∴△CAP∽△CMA
∴AC2=CPCM
∵AC=![]() AB
AB
∴2CB2=CPCM

练习册系列答案
相关题目
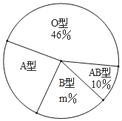
【题目】“只要人人献出一点爱,世界将变成美好的人间”.某大学利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A、B、AB、O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表,图):
血型统计表
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)本次随机抽取献血者人数为 人,图中m= ;
(2)补全表中的数据;
(3)若这次活动中该校有1300人义务献血,估计大约有多少人是A型血?
(4)现有4个自愿献血者,2人为O型,1人为A型,1人为B型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为O型的概率.