题目内容
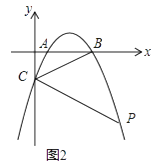
【题目】如图,三角形A′B′C′是三角形ABC经过某种变换后得到的图形.
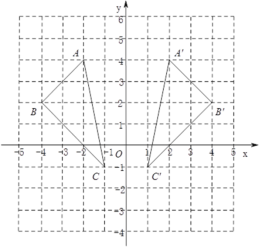
(1)分别写出点A和点A′,点B和点B′,点C和点C′的坐标;
(2)观察点A和点A′,点B和点B′,点C和点C′的坐标,用文字语言描述它们的坐标之间的关系 ;
(3)三角形ABC内任意一点M的坐标为(x,y),点M经过这种变换后得到点M′,则点M′的坐标为 .
【答案】解:(1)A(-2,4),A′(2,4),B(-4,2),B′(4,2),C(-1,-1),C′(1,-1);(2)横坐标互为相反数,纵坐标相等;(3)(-x,y)
【解析】
(1)根据点的位置写出坐标即可;
(2)探究规律,利用规律解决问题即可;
(3)利用(2)中结论解决问题即可.
解:(1)A(-2,4),A′(2,4),B(-4,2),B′(4,2),C(-1,-1),C′(1,-1);
(2)观察可知:横坐标互为相反数,纵坐标相等
故答案为:横坐标互为相反数,纵坐标相等;
(3)三角形ABC内任意一点M的坐标为(x,y),点M经过这种变换后得到点M则点![]() 的坐标为(-x,y).
的坐标为(-x,y).
故答案为:(-x,y).

练习册系列答案
相关题目