题目内容
如图，以正方形ABCD的对角线AC为一边，延长AB到E，使AE=AC，以AE为一边作菱形AEFC，若菱形的面积为9| 2 |
分析：根据题意可知AC=AE，且CB⊥AE，故菱形面积S=AE•BC，且AC=
BC，根据S可求得BC的值，且BC为正方形的边长，即可解题．
| 2 |
解答：解：正方形边长为BC，
则对角线AC=
BC，
且AE=AC，
∴AE=
BC，
∵菱形面积S=AE•BC
∴
BC•BC=9
，
∴BC=3．
故正方形的边长为 3．
则对角线AC=
| 2 |
且AE=AC，
∴AE=
| 2 |
∵菱形面积S=AE•BC
∴
| 2 |
| 2 |
∴BC=3．
故正方形的边长为 3．
点评：本题考查了正方形各边长相等、各内角为直角的性质，菱形面积的计算，菱形各边长相等的性质，本题中求证AE=
BC是解题的关键．
| 2 |
练习册系列答案
相关题目
13、如图，以直角△ABC的三边向外作正方形，其面积分别为S1，S2，S3且S1=4，S2=8，则S3=
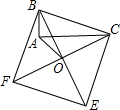如图，以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF，设正方形的中心为O，连接AO，如果AB=4，AO=6
如图，以Rt△ABC的斜边BC为一边作正方形BCDE，设正方形的中心为O，连接AO，如果AB=3，AO=
如图，以Rt△ABC的斜边和一直角边为边长向外作正方形，面积分别为169和25，则另一直角边的长度BC为（ ）
如图，以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3，且S1+S2+S3=50，则AB=（ ）