题目内容
如下图,在直角坐标系中,M为![]() 轴上一点,⊙M交
轴上一点,⊙M交![]() 轴于A、B两点,交
轴于A、B两点,交![]() 轴于C、D两点,P为BC上的一个动点,CQ平分∠PCD,A(-1,0),如(1,0)。
轴于C、D两点,P为BC上的一个动点,CQ平分∠PCD,A(-1,0),如(1,0)。
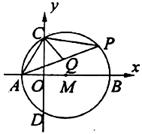
(1)求C点的坐标;
(2)当P点运动时,线段AQ的长度是否改变?若不变,请求其值;若改变请说明理由。
(1)解:连接MC
由A(-1,0),M(1,0)可知,
OA=OM=1,MA=2
在Rt△OCM中,OC=![]()
∴点C的坐标是(0,![]() )
)
(2)答:当P点运动时,线段AQ的长度不改变。
由垂径定理知:AC=AD
∴∠P=∠ACD
∵CQ平分∠PCD
∴∠P+∠PCQ=∠ACD+∠DCQ
即:∠ACQ=∠AQC
∴AQ=AC
在Rt△OCA中,OC=![]() ,OA=1
,OA=1
∴ AC=2
线段AQ的长度为2

练习册系列答案
相关题目
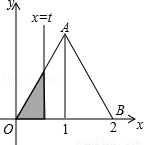
 如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )
如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )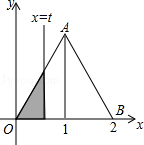



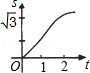




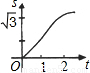
 B.
B. C.
C. D.
D.