题目内容
⊙O1和⊙O2的圆心距为7，有4个完全一样的小圆球，分别标有数字2、3、4、5，从4个球中任意取2个球（无放回），以球上的数字作为两圆的半径，则两圆相切的概率为
- A.
- B.
- C.
- D.
C
分析：首先根据题意列树状图，然后由树状图求得所有等可能的结果与两圆相切的情况数，再利用概率公式求解即可求得答案．
解答：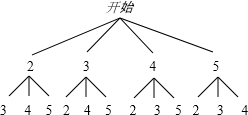
解：画树状图得：
∴一共有12种等可能的结果，
∵⊙O1和⊙O2的圆心距为7，
∴两圆相切的有（2，5），（3，4），（4，3），（5，2）共4种情况，
∴两圆相切的概率为：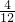
=．
故选C．
点评：此题考查了圆与圆的位置关系与树状图法或列表法求概率的知识．此题难度不大，解题的关键是掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系与概率公式的应用．
分析：首先根据题意列树状图，然后由树状图求得所有等可能的结果与两圆相切的情况数，再利用概率公式求解即可求得答案．
解答：
解：画树状图得：∴一共有12种等可能的结果，
∵⊙O1和⊙O2的圆心距为7，
∴两圆相切的有（2，5），（3，4），（4，3），（5，2）共4种情况，
∴两圆相切的概率为：
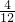=．故选C．
点评：此题考查了圆与圆的位置关系与树状图法或列表法求概率的知识．此题难度不大，解题的关键是掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系与概率公式的应用．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
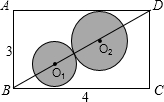如图，矩形纸片ABCD中，AB=3cm，BC=4cm，若要在该纸片中剪下两个外切的圆⊙O1和⊙O2，要求⊙O1和⊙O2的圆心均在对角线BD上，且⊙O1和⊙O2分别与BC、AD相切，则O1O2的长为（ ）A、
| ||
B、
| ||
C、
| ||
| D、2cm |
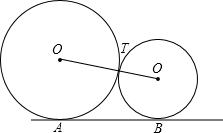如图，⊙O1和⊙O2外切于点T，它们的半径之比为3：2，AB是它们的外公切线，A、B是切点，AB=4| 6 |
A、5
| ||||
B、10
| ||||
| C、10 | ||||
D、
|
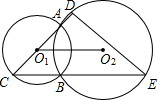AC=6cm，BE=11cm，AD=BC．求：