题目内容
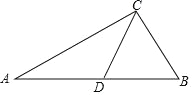
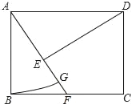
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为直径作圆,交斜边AB于点E,D为AC的中点.连接DO,DE.则下列结论中不一定正确的是( )

A. DO∥ABB. △ADE是等腰三角形
C. DE⊥ACD. DE是⊙O的切线
【答案】C
【解析】
连接OE,由OD为三角形ABC的中位线,利用中位线定理得到OD与AB平行,选项A正确;由两直线平行得到同位角相等,内错角相等即∠COD=∠B,∠DOE=∠OEB,再由OE=OB,利用等边对等角得到∠OEB=∠B,等量代换得到∠COD=∠DOE,再由OC=OE,OD为公共边得到三角形COD与三角形EOD全等,由全等三角形的对应角相等得到∠OED=∠OCD为直角,即OE垂直于DE,可得出DE为圆O的切线,选项D正确;连接EC,由BC是直径可得∠AEC=∠CEB=90°,在直角三角形AEC中,D为斜边的中点,根据直角三角形斜边上的中线等于斜边的一半可得DE=AD,即三角形AED为等腰三角形,选项B正确,而DE不一定垂直于AC,故选项C符合题意.
连接OE
∵D为AC中点,O为BC中点
∴OD为△ABC的中位线,
∴DO∥AB,选项A正确;
∵∠COD=∠B,∠DOE=∠OEB,
∵OE=OB,
∴∠OEB=∠B,
∴∠COD=∠DOE,
在△COD和△EOD中,
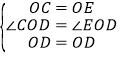 ,
,
∴△COD≌△EOD(SAS),
∴∠OED=∠OCD=90°,
∴DE为圆O的切线,选项D正确;
连接EC,∵BC是直径,
∴∠AEC=∠CEB=90°,
在RtAEC中,
∵AD=DC,
∴DE=AD,
∴△AED为等腰三角形,选项B正确,
则不一定正确的为DE⊥AC.
故选:C.


练习册系列答案
相关题目