题目内容
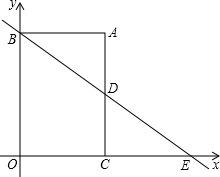 已知如图,四边形ABOC为矩形,AB=4,AC=6,一次函数经过B点与反比例函数交于D点,与x轴交于E点,且D为AC的中点.
已知如图,四边形ABOC为矩形,AB=4,AC=6,一次函数经过B点与反比例函数交于D点,与x轴交于E点,且D为AC的中点.①求点D和点E的坐标;
②求一次函数和反比例函数的解析式;
③在x轴上是否存在点P,使△PBD的周长最小?若存在,求出点P的坐标和△PBD的周长;若不存在,请说明理由.
分析:①根据D为AC的中点且AC=6求得CD=3,根据AB=OC=4,从而得到点D的坐标,然后根据全等三角形求得CE=AB=4,从而得到OE=8,进而得到点E的坐标;
②利用待定系数法分别根据求得的点的坐标求得一次函数与反比例函数的解析式即可;
③因BD长度固定,要使△PBD周长最小,只需PB+PD最小.作D关于x轴的对称点D′,连接BD′,交x轴于P点,根据对称性及两点之间线段最短说明存在P点.
②利用待定系数法分别根据求得的点的坐标求得一次函数与反比例函数的解析式即可;
③因BD长度固定,要使△PBD周长最小,只需PB+PD最小.作D关于x轴的对称点D′,连接BD′,交x轴于P点,根据对称性及两点之间线段最短说明存在P点.
解答:解:①∵AC=6,D为AC的中点,
∴CD=3,
∵AB=OC=4,
∴点D的坐标为(4,3),
在△ABD与△ECD中,
,
∴△ABD≌△ECD(ASA),
∴CE=AB=4,
∴点E的坐标为(8,0),
②∵OB=AC=6,
∴点B的坐标为(0,6)
设一次函数的解析式为y=k1x+b,
∵经过点B和点E,
∴
,
解得:
,
∴一次函数的解析式为y=-
x+6,
设反比例函数的解析式为y=
,
∵经过点D(4,3)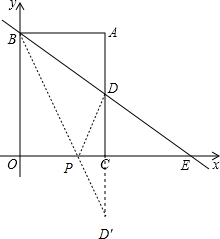 ,
,
∴k2=3×4=12,
∴反比例函数的解析式为y=
;
③△PBD中,BD恒等于10,要使△PBD周长最小,即要使BP+PD最小.
如图,作D关于x轴对称点D′,连BD′交x轴于点P,连PD,此时,△PBD周长最小.
∵D(4,3),
∴D'(4,-3),
∴AB=4,AD′=9,
∴由勾股定理得BD′=
=
,
∵AD′∥BO,
∴△OBP∽△CD′P,
∴
=
=
,
即:
=
,
∵OC=4,
∴PO=
OC=
,
∴点P的坐标为(
,0).
此时△PBD的周长为BD+BD′=5+
.
∴CD=3,
∵AB=OC=4,
∴点D的坐标为(4,3),
在△ABD与△ECD中,
|
∴△ABD≌△ECD(ASA),
∴CE=AB=4,
∴点E的坐标为(8,0),
②∵OB=AC=6,
∴点B的坐标为(0,6)
设一次函数的解析式为y=k1x+b,
∵经过点B和点E,
∴
|
解得:
|
∴一次函数的解析式为y=-
| 3 |
| 4 |
设反比例函数的解析式为y=
| k2 |
| x |
∵经过点D(4,3)
 ,
,∴k2=3×4=12,
∴反比例函数的解析式为y=
| 12 |
| x |
③△PBD中,BD恒等于10,要使△PBD周长最小,即要使BP+PD最小.
如图,作D关于x轴对称点D′,连BD′交x轴于点P,连PD,此时,△PBD周长最小.
∵D(4,3),
∴D'(4,-3),
∴AB=4,AD′=9,
∴由勾股定理得BD′=
| 42+92 |
| 97 |
∵AD′∥BO,
∴△OBP∽△CD′P,
∴
| PO |
| PC |
| PB |
| PD′ |
| CD′ |
| BO |
即:
| PO |
| PC |
| 2 |
| 1 |
∵OC=4,
∴PO=
| 2 |
| 3 |
| 8 |
| 3 |
∴点P的坐标为(
| 8 |
| 3 |
此时△PBD的周长为BD+BD′=5+
| 97 |
点评:本题考查了反比例函数的综合应用,坐标系内求点的坐标、利用作图求最小值等知识点,综合性很强,利用轴对称得出△PDB周长最小时P的位置是解题关键.

练习册系列答案
相关题目
 20、已知如图,四边形ABCD中,AB=BC,∠A=∠C,求证:AD=CD.
20、已知如图,四边形ABCD中,AB=BC,∠A=∠C,求证:AD=CD. 22、(A类)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠C.
22、(A类)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠C. 23、已知如图平行四边形ABCD,分别以AB,BC为边作等边△EAB与等边△FBC,连接EF,DF与DE,猜想△DEF的形状并加以证明.
23、已知如图平行四边形ABCD,分别以AB,BC为边作等边△EAB与等边△FBC,连接EF,DF与DE,猜想△DEF的形状并加以证明.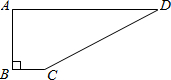 已知如图,四边形ABCD中,∠B=90°,AB=4,BC=3,CD=12,AD=13,求这个四边形的面积.
已知如图,四边形ABCD中,∠B=90°,AB=4,BC=3,CD=12,AD=13,求这个四边形的面积.