题目内容
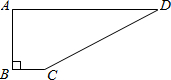 已知如图,四边形ABCD中,∠B=90°,AB=4,BC=3,CD=12,AD=13,求这个四边形的面积.
已知如图,四边形ABCD中,∠B=90°,AB=4,BC=3,CD=12,AD=13,求这个四边形的面积.分析:连接AC,在直角三角形ABC中,由AB及BC的长,利用勾股定理求出AC的长,再由AD及CD的长,利用勾股定理的逆定理得到三角形ACD为直角三角形,根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积,即可求出四边形的面积.
解答:解:连接AC,如图所示:
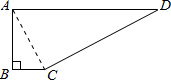
∵∠B=90°,∴△ABC为直角三角形,
又AB=4,BC=3,
∴根据勾股定理得:AC=
=5,
又AD=13,CD=12,
∴AD2=132=169,CD2+AC2=122+52=144+25=169,
∴CD2+AC2=AD2,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACD=
AB•BC+
AC•CD=
×3×4+
×12×5=36.

∵∠B=90°,∴△ABC为直角三角形,
又AB=4,BC=3,
∴根据勾股定理得:AC=
| AB2+BC2 |
又AD=13,CD=12,
∴AD2=132=169,CD2+AC2=122+52=144+25=169,
∴CD2+AC2=AD2,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了勾股定理,以及勾股定理的逆定理,熟练掌握定理及逆定理是解本题的关键.

练习册系列答案
相关题目
 20、已知如图,四边形ABCD中,AB=BC,∠A=∠C,求证:AD=CD.
20、已知如图,四边形ABCD中,AB=BC,∠A=∠C,求证:AD=CD. 22、(A类)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠C.
22、(A类)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠C. 23、已知如图平行四边形ABCD,分别以AB,BC为边作等边△EAB与等边△FBC,连接EF,DF与DE,猜想△DEF的形状并加以证明.
23、已知如图平行四边形ABCD,分别以AB,BC为边作等边△EAB与等边△FBC,连接EF,DF与DE,猜想△DEF的形状并加以证明.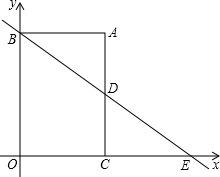 已知如图,四边形ABOC为矩形,AB=4,AC=6,一次函数经过B点与反比例函数交于D点,与x轴交于E点,且D为AC的中点.
已知如图,四边形ABOC为矩形,AB=4,AC=6,一次函数经过B点与反比例函数交于D点,与x轴交于E点,且D为AC的中点.