题目内容
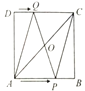
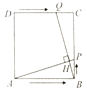
【题目】如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.
(1)请写出图中各对相似三角形(相似比为1除外);
(2)求BP:PQ:QR.

【答案】(1)见解析;(2)3:1:2
【解析】试题分析:
(1)由平行四边形的性质结合相似三角形的判定定理可证得:①△BCP∽△BER;②△PCQ∽△RDQ;③△PCQ∽△PAB;④△PAB∽△RDQ;
(2)由(1)已知条件易证![]() ,结合R是DE的中点,易得
,结合R是DE的中点,易得![]() ,设BR=
,设BR= ![]() ,则BP=
,则BP= ![]() ,PQ=
,PQ= ![]() ,QR=
,QR= ![]() ,由此即可求得BP:PQ:QR的比值.
,由此即可求得BP:PQ:QR的比值.
试题解析:
(1)①∵四边形ACED是平行四边形,
∴∠BPC=∠BRE,∠BCP=∠E,
∴△BCP∽△BER;
②同理可得∠CDE=∠ACD,∠PQC=∠DQR,
∴△PCQ∽△RDQ;
③∵四边形ABCD是平行四边形,
∴∠BAP=∠PCQ,
∵∠APB=∠CPQ,
∴△PCQ∽△PAB;
④∵△PCQ∽△RDQ,△PCQ∽△PAB,
∴△PAB∽△RDQ.
综上所述,图中共有4对相似三角形,分别是:①△BCP∽△BER;②△PCQ∽△RDQ;③△PCQ∽△PAB;④△PAB∽△RDQ;
(2)∵四边形ABCD和四边形ACED都是平行四边形,
∴BC=AD=CE,
∵△BCP∽△BER,△PCQ∽△RDQ,
∴![]() ,
, ![]() ,
,
∵R是DE的中点,
∴RE=DR,
∴![]()
∴当设BR= ![]() 时,BP=
时,BP= ![]() ,PQ=
,PQ= ![]() ,QR=
,QR= ![]() ,
,
∴BP:PQ:QR= ![]() :
: ![]() :
: ![]() =3:1:2.
=3:1:2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目