题目内容
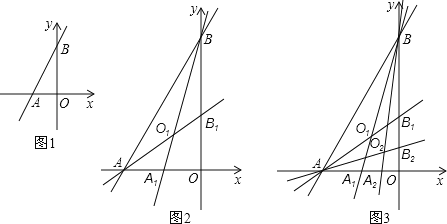
【题目】(1)如图1,已知![]() ,
,![]() ,可得
,可得![]() =______;
=______;
(2)如图2,在(1)的条件下,如果![]() 平分
平分![]() ,则
,则![]() =________;
=________;
(3)如图3,在(1)(2)的条件下,如果![]() ,则
,则![]() =_________;
=_________;
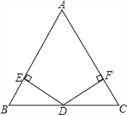
(4)尝试解决下面问题:如图4,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,求
,求![]() 的度数.
的度数.




【答案】 60° 30° 60°
【解析】分析:(1)∠BCD与∠ABC是两平行直线AB、CD被BC所截得到的内错角,所以根据两直线平行,内错角相等即可求解;
(2)根据角平分线的定义求解即可;
(3)根据互余的两个角的和等于90°,计算即可;
(4)先根据两直线平行,同旁内角互补和角平分线的定义求出∠BCN的度数,再利用互余的两个角的和等于90°即可求出.
详解:(1)∵AB//CD,∴∠BCD=∠B=60°.
故答案为:60°;
(2)∵CM平分∠BCD,∴∠BCN=![]() ∠BCD=
∠BCD=![]() ×60°=30°.
×60°=30°.
故答案为:30°;
(3)∵CN⊥CM,∴∠MCN=90°,∴∠BCN=90°-∠BCM=90°-30°=60°.故答案为:60°;
(4)∵AB∥CD,∴∠B+∠BCE=180°.
∵∠B=40°,∴∠BCE=180°﹣∠B=180°﹣40°=140°.
又∵CN是∠BCE的平分线,∴∠BCN=140°÷2=70°.
∵CN⊥CM,∴∠BCM=90°﹣∠BCN=90°﹣70°=20°.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目