题目内容
【题目】如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,求∠A的度数.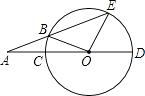
【答案】解:设∠A=x°,
∵AB=OC,OC=OB,
∴AB=OB,
∴∠AOB=∠A=x°,
∴∠OBE=∠A+∠AOB=2x°,
∵OB=OE,
∴∠E=∠OBE=2x°,
∴∠EOD=∠A+∠E=3x°=72°,
∴∠A=24°.
【解析】由AB=OC,OC=OB,得出AB=OB,根据等边对等角得出∠AOB=∠A,根据三角形的外角得出∠OBE=∠A+∠AOB,又有OB=OE,故∠E=∠OBE从而得出方程求解即可。
【考点精析】掌握三角形的外角和等腰三角形的性质是解答本题的根本,需要知道三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;等腰三角形的两个底角相等(简称:等边对等角).

练习册系列答案
相关题目