题目内容
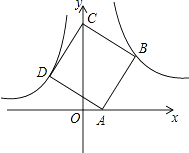
【题目】如图,已知直线y=﹣ ![]() x+2与抛物线y=a (x+2)2相交于A、B两点,点A在y轴上,M为抛物线的顶点.
x+2与抛物线y=a (x+2)2相交于A、B两点,点A在y轴上,M为抛物线的顶点.
(1)请直接写出点A的坐标及该抛物线的解析式;
(2)若P为线段AB上一个动点(A、B两端点除外),连接PM,设线段PM的长为l,点P的横坐标为x,请求出l2与x之间的函数关系,并直接写出自变量x的取值范围;
(3)在(2)的条件下,线段AB上是否存在点P,使以A、M、P为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:A的坐标是(0,2),抛物线的解析式是y= ![]() (x+2)2.
(x+2)2.
联立直线与抛物线解析式可得B点坐标为(﹣5, ![]() )
)
(2)
解:如图,P为线段AB上任意一点,连接PM,
过点P作PD⊥x轴于点D,
设P的坐标是(x,﹣ ![]() x+2),则在Rt△PDM中,
x+2),则在Rt△PDM中,
PM2=DM2+PD2
即l2=(﹣2﹣x)2+(﹣ ![]() x+2)2=
x+2)2= ![]() x2+2x+8,
x2+2x+8,
P为线段AB上一个动点,故自变量x的取值范围为:﹣5<x<0,
答:l2与x之间的函数关系是l2= ![]() x2+2x+8,自变量x的取值范围是﹣5<x<0.
x2+2x+8,自变量x的取值范围是﹣5<x<0.
(3)
解:存在满足条件的点P,
连接AM,
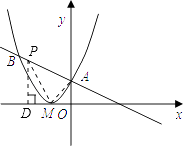
由题意得,AM= ![]() =2
=2 ![]() ,
,
①当PM=PA时, ![]() x2+2x+8=x2+(﹣
x2+2x+8=x2+(﹣ ![]() x+2﹣2)2,
x+2﹣2)2,
解得:x=﹣4,
此时y=﹣ ![]() ×(﹣4)+2=4,
×(﹣4)+2=4,
∴点P1(﹣4,4);
②当PM=AM时, ![]() x2+2x+8=(2
x2+2x+8=(2 ![]() )2,
)2,
解得:x1=﹣ ![]() x2=0(舍去),
x2=0(舍去),
此时y=﹣ ![]() ×(﹣
×(﹣ ![]() )+2=
)+2= ![]() ,
,
∴点P2(﹣ ![]() ,
, ![]() ),
),
③当PA=AM时,x2+(﹣ ![]() x+2﹣2)2=(2
x+2﹣2)2=(2 ![]() )2,
)2,
解得:x1=﹣ ![]() x2=
x2= ![]() (舍去),
(舍去),
此时y=﹣ ![]() ×(﹣
×(﹣ ![]() )+2=
)+2= ![]() ,
,
∴点P3(﹣ ![]() ,
, ![]() ),
),
综上所述,满足条件的点为:
P1(﹣4,4)、P2(﹣ ![]() ,
, ![]() )、P3(﹣
)、P3(﹣ ![]() ,
, ![]() ),
),
答:存在点P,使以A、M、P为顶点的三角形是等腰三角形,点P的坐标是(﹣4,4)或(﹣ ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() ).
).
【解析】(1)把x=0代入求出A的坐标,求出直线与抛物线的交点坐标即可;(2)过点P作PD⊥x轴于点D,设P的坐标是(x,﹣ ![]() x+2),根据勾股定理求出x即可;(3)连接AM,求出AM,①当PM=PA时,根据勾股定理得到
x+2),根据勾股定理求出x即可;(3)连接AM,求出AM,①当PM=PA时,根据勾股定理得到 ![]() x2+2x+8=x2+(﹣
x2+2x+8=x2+(﹣ ![]() x+2﹣2)2 , 求出方程的解即可;同理②当PM=AM时,求出P的坐标;③当PA=AM时,求出P的坐标.
x+2﹣2)2 , 求出方程的解即可;同理②当PM=AM时,求出P的坐标;③当PA=AM时,求出P的坐标.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5. 月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?