题目内容
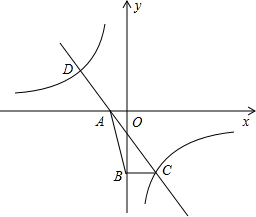 (2013•德阳)如图,直线y=kx+k(k≠0)与双曲线y=
(2013•德阳)如图,直线y=kx+k(k≠0)与双曲线y=| n+1 |
| x |
(1)求n的取值范围和点A的坐标;
(2)过点C作CB⊥y轴,垂足为B,若S△ABC=4,求双曲线的解析式;
(3)在(1)(2)的条件下,若AB=
| 17 |
分析:(1)由反比例函数图象位于第二、四象限,得到比例系数小于0列出关于n的不等式,求出不等式的解集即可得到n的范围,对于直线解析式,令y=0求出x的值,确定出A的坐标即可;
(2)设C(a,b),表示出三角形ABC的面积,根据已知的面积列出关于a与b的关系式,利用反比例函数k的几何意义即可求出k的值,确定出反比例解析式;
(3)由CB垂直于y轴,得到B,C纵坐标相同,即B(0,b),在直角三角形AOB中,由AB与OA的长,利用勾股定理求出OB的长,确定出B坐标,进而确定出C坐标,将C代入直线解析式求出k的值,确定出一次函数解析式,与反比例解析式联立求出D的坐标,由C,D两点的横坐标,利用图象即可求出反比例函数的值小于一次函数的值时,自变量x的取值范围.
(2)设C(a,b),表示出三角形ABC的面积,根据已知的面积列出关于a与b的关系式,利用反比例函数k的几何意义即可求出k的值,确定出反比例解析式;
(3)由CB垂直于y轴,得到B,C纵坐标相同,即B(0,b),在直角三角形AOB中,由AB与OA的长,利用勾股定理求出OB的长,确定出B坐标,进而确定出C坐标,将C代入直线解析式求出k的值,确定出一次函数解析式,与反比例解析式联立求出D的坐标,由C,D两点的横坐标,利用图象即可求出反比例函数的值小于一次函数的值时,自变量x的取值范围.
解答:解:(1)由图象得:n+1<0,
解得:n<-1,
由y=kx+k,令y=0,解得:x=-1,
则A坐标为(-1,0);
(2)设C(a,b),
∵S△ABC=
a•(-b)=4,
∴ab=-8,
∵点C在双曲线上,
∴y=-
;
(3)∵CB⊥y轴,∴B(0,b),
在Rt△AOB中,AB=
,OA=1,
根据勾股定理得:OB=4,
∴B(0,-4),
∴C(2,-4),
将C代入直线y=kx+k中,得:2k+k=-4,即k=-
,
∴直线AC解析式为y=-
x-
,
联立直线与反比例解析式得:
,
解得:
或
,
∴D(-3,
),
则由图象可得:当x<-3或0<x<2时,反比例函数的值小于一次函数的值.
解得:n<-1,
由y=kx+k,令y=0,解得:x=-1,
则A坐标为(-1,0);
(2)设C(a,b),
∵S△ABC=
| 1 |
| 2 |
∴ab=-8,
∵点C在双曲线上,
∴y=-
| 8 |
| x |
(3)∵CB⊥y轴,∴B(0,b),
在Rt△AOB中,AB=
| 17 |
根据勾股定理得:OB=4,
∴B(0,-4),
∴C(2,-4),
将C代入直线y=kx+k中,得:2k+k=-4,即k=-
| 4 |
| 3 |
∴直线AC解析式为y=-
| 4 |
| 3 |
| 4 |
| 3 |
联立直线与反比例解析式得:
|
解得:
|
|
∴D(-3,
| 8 |
| 3 |
则由图象可得:当x<-3或0<x<2时,反比例函数的值小于一次函数的值.
点评:此题考查了反比例函数与一次函数的交点问题,利用了待定系数法,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
 (2013•德阳)如图,⊙O的直径CD过弦EF的中点G,∠DCF=20°,则∠EOD等于( )
(2013•德阳)如图,⊙O的直径CD过弦EF的中点G,∠DCF=20°,则∠EOD等于( ) (2013•德阳)如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )
(2013•德阳)如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )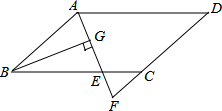 (2013•德阳)如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=
(2013•德阳)如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=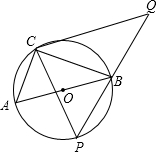 (2013•德阳)如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为
(2013•德阳)如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为