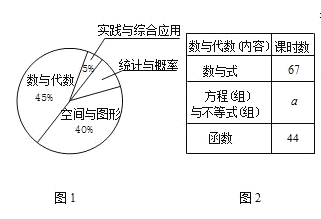
题目内容
【题目】二次函数 ![]() 的部分图像如图所示,图像过点
的部分图像如图所示,图像过点 ![]() ,对称轴为直线
,对称轴为直线 ![]() ,下列结论:(1)
,下列结论:(1) ![]() ;(2)
;(2) ![]() ;(3)若点
;(3)若点 ![]() 、点
、点 ![]() 、点
、点 ![]() 在该函数图像上,则
在该函数图像上,则 ![]() ;(4)若方程
;(4)若方程 ![]() 的两根为
的两根为 ![]() 和
和 ![]() ,且
,且 ![]() ,则
,则 ![]() .其中正确结论的序号是.
.其中正确结论的序号是.
【答案】(1)(4)
【解析】:∵抛物线的对称轴为直线x=- ![]() =2,∴b=-4a>0,即4a+b=0,所以(1)正确;∵x=-3时,y<0,∴9a-3b+c<0,即9a+c<3b,所以(2)错误;∵抛物线的对称轴为直线x=-
=2,∴b=-4a>0,即4a+b=0,所以(1)正确;∵x=-3时,y<0,∴9a-3b+c<0,即9a+c<3b,所以(2)错误;∵抛物线的对称轴为直线x=- ![]() =2,图象与x轴交于(-1,0),
=2,图象与x轴交于(-1,0),
∴抛物线x轴的另一个交点是(5,0),∵点A(-3,y1)、点B(- ![]() ,y2)、点C(
,y2)、点C( ![]() ,y3),∵
,y3),∵ ![]() -2=
-2= ![]() ,2-(-
,2-(- ![]() )=
)= ![]() ,∴
,∴ ![]() <
< ![]() ∴点C离对称轴的距离近,∴y3>y2,∵a<0,-3<-
∴点C离对称轴的距离近,∴y3>y2,∵a<0,-3<- ![]() <2,∴y1<y2∴y1<y2<y3,故(3)错误.如图,
<2,∴y1<y2∴y1<y2<y3,故(3)错误.如图,
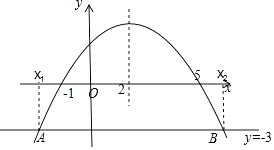
∵a<0,∴(x+1)(x-5)=-3/a>0,即(x+1)(x-5)>0,故x<-1或x>5,故(4)正确.
由抛物线的对称轴直线,得到4a+b=0,图象与x轴交于(-1,0),得到抛物线x轴的另一个交点,由已知得到点C离对称轴的距离近,得到y3>y2,由a<0,得到y1<y2<y3.

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度 | …… | -4 | -2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
这些数据说明:植物每天高度增长量 ![]() 关于温度
关于温度 ![]() 的函数是反比例函数、一次函数和二次函数中的一种.
的函数是反比例函数、一次函数和二次函数中的一种.
(1)你认为是哪一种函数,并求出它的函数关系式;
(2)温度为多少时,这种植物每天高度增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度x应该在哪个范围内选择?请直接写出结果.