题目内容
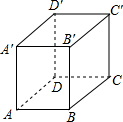
如图,正四棱柱的底面边长为5 cm,侧棱长为8 cm,一只蚂蚁欲从正四棱柱底面上的顶点 A沿棱柱的表面到顶点C′处吃食物. 那么它需要爬行的最短路程的长是多少?
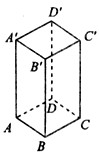
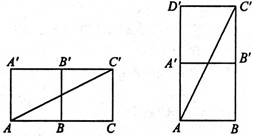
图1 图2
解:(1)沿侧枝 BB',将侧面A'B和侧面B'C展开如图1所示,连接AC'.
∵AB=BC=5 cm,CC'=8 cm,
由勾股定理,得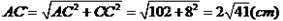
(2)沿底边A'B'. 将底面A'C'和侧面A'B展开如图2所示,连接 AC'.
∵AB=5cm,BC’=BB’+B’C’=8+5=13cm,
由勾股定理,得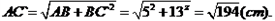
易知沿 DC展开和DD'展开的情况同上述两种情况一致.
又∵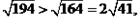
∴蚂蚁需要爬行的最短路轻的长为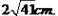
∵AB=BC=5 cm,CC'=8 cm,
由勾股定理,得
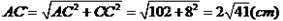
(2)沿底边A'B'. 将底面A'C'和侧面A'B展开如图2所示,连接 AC'.
∵AB=5cm,BC’=BB’+B’C’=8+5=13cm,
由勾股定理,得
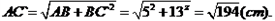
易知沿 DC展开和DD'展开的情况同上述两种情况一致.
又∵
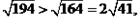
∴蚂蚁需要爬行的最短路轻的长为
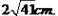

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
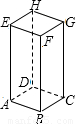
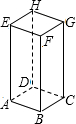 如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲从顶点A沿棱柱侧面爬到顶点G处吃食物,那么它需爬行的最短路径是
如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲从顶点A沿棱柱侧面爬到顶点G处吃食物,那么它需爬行的最短路径是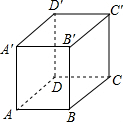 如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲 从正四棱柱的底面上的点A 沿棱柱表面到点C处吃食物,那么它所爬行的最短路径的长为
如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲 从正四棱柱的底面上的点A 沿棱柱表面到点C处吃食物,那么它所爬行的最短路径的长为