题目内容
如图,Q为正方形ABCD的边CD的中点,P为BC边上一点(不与B、C重合),当P点满足条件 时,有AQ⊥PQ.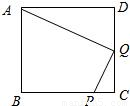
【答案】分析:把AQ⊥PQ作为已知条件,则∠CQP=∠DAQ,即△AQD∽△QPC,根据比例线段即可求解.
解答:解:∵AQ⊥PQ,
∴∠CQP=∠DAQ,
∵∠D=∠C,
∴△AQD∽△QPC,
∴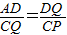 ,
,
∵Q为正方形ABCD的边CD的中点,
∴CP= CQ,
CQ,
∴CP= CB.
CB.
点评:本题考查了正方形的性质,属于探究性试题,解决这类题可以把结论作为已知条件来求解.
解答:解:∵AQ⊥PQ,
∴∠CQP=∠DAQ,
∵∠D=∠C,
∴△AQD∽△QPC,
∴
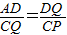 ,
,∵Q为正方形ABCD的边CD的中点,
∴CP=
 CQ,
CQ,∴CP=
 CB.
CB.点评:本题考查了正方形的性质,属于探究性试题,解决这类题可以把结论作为已知条件来求解.

练习册系列答案
相关题目
 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合. OM方向以
OM方向以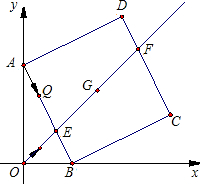 向以
向以
 (2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.
(2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.