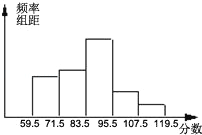
题目内容
【题目】如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交![]() 轴于点
轴于点![]() ,且
,且![]() ,
,![]() 满足
满足![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
(1)![]() ________;
________;![]() ________;并求直线
________;并求直线![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

【答案】(1)4,2,![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)先根据非负数的性质可求得a,b的值,利用待定系数法可求得直线AB的解析式;
(2)先求得点M的坐标,过M点作MN⊥OA于点N,MP⊥OB于点P,由题设可证△MNA≌△MPC,△OMN≌△OMP,利用全等的性质可分别求得CP的长,从而求得点C的坐标;
(3)先假设存在点D,设D(a,a),根据S△ABD=6,列出关于a方程,若有解则存在,无解则不存在,要注意分两种情况考虑.
(1)∵![]()
∴a-4=0,b-2=0
即a=4,b=2
∴A(4,0),B(0,2)
设直线AB的解析式为y=kx+b,将![]() ,
,![]() 代入
代入![]() 得
得
![]() ,
,
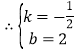
![]() 直线
直线![]() 解析式为
解析式为![]()
(2)联立方程组得,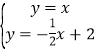 ,
,
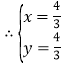 ,
,
即![]()
如图1,过M点作MN⊥OA于点N,MP⊥OB于点P,
则四边形OPMN是矩形,
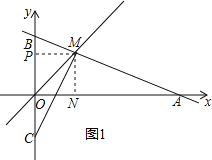
由点M的坐标可知MN=MP,
∴矩形OPMN是正方形,
∴∠PMN=90°,∠MPC=∠MNA=90°,
又∠OMA=90°,
∴∠PMC=∠NMA,
∴△MNA≌△MPC,△OMN≌△OMP,
则CP=AN,OP=ON=![]() ,
,
而CP=AN=OA-ON=![]() ,
,
故OC=![]() ,
,
所以C(0,![]() );
);
(3)存在点D.
∵D在y=x上
∴设D(a,a)
①如图2,若D在AB的下方,
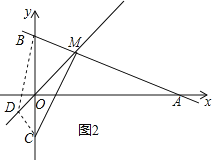
∵S△AOB=4,S△ABD=6
∴D在MO的延长线上
∴S△AOD+S△BOD+S△AOB=S△ABD,
∴![]() (AO+BO)|a|+4=6,
(AO+BO)|a|+4=6,
∴-![]() ×6a=2,
×6a=2,
解得:a=-![]() ,
,
∴D(![]() ,
,![]() )
)
②若D在AB的上方同理求得D′(![]() ,
,![]() ).
).

【题目】如表:方程1、方程2、方程3…是按照一定规律排列的一列方程:
序号 | 方程 | 方程的解 |
1 |
| x1=3,x2=4 |
2 |
| x1=4,x2=6 |
3 |
| x1=5,x2=8 |
… | … | … |
(1)若方程![]() ﹣
﹣![]() =1(a>b)的解是x1=6,x2=10,则a=_____b=_____.
=1(a>b)的解是x1=6,x2=10,则a=_____b=_____.
(2)请写出这列方程中第n个方程:_____ 方程的解:_____.