Question

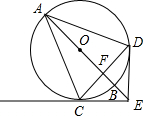AB是⊙O的直径，AC是⊙O的弦，过C作⊙O的切线，交AB的延长线于E．作弦AD，使∠DAB=∠CAB，连接ED．
（1）求证：ED是⊙O的切线；
（2）当∠CAD=

 

°时，CE⊥DE，证明你的结论；
（3）CD与AE相交于F，当OF=2，FB=3时，求E到⊙O的切线长．

Answer 1

分析：（1）连接OC，OD．要证明ED是⊙O的切线，只需证明∠ODE=90°即可；
（2）结合（1）中切线的性质和CE⊥DE，OC=OD，可知四边形OCED是正方形，则∠COD=90°，根据圆周角定理得到∠CAD=45°；
（3）根据等腰三角形COD的三线合一，得到OB垂直平分CD．根据相交弦定理即可求得CF的长，再根据勾股定理和切割线定理进行列方程组求解．

解答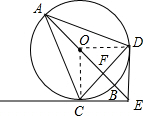：证明：（1）连接OC，OD；
∵CE是圆的切线，
∴∠OCE=90°．
∵∠DAB=∠CAB，
∴∠COE=∠DOE．
∵OC=OD，OE=OE，
∴△COE≌△DOE．
∴∠ODE=∠OCE=90°．
∴ED是⊙O的切线．

（2）45°．
∵∠COD=90°，
∴四边形OCED为正方形．
∴CE⊥DE．

（3）根据题意，得圆的半径是5，则AF=7，
∵OC=OD，∠COE=∠DOE，
∴OB垂直平分CD．
∵CF•DF=AF•FB=21，CF=DF=

21

，
设CE=x，BE=y，
则有

x2=21+(3+y)2 x2=y(y+10)

，
解得

x= 5 2 21 y=7.5

，
即CE=

5

2

21

．

点评：此题综合运用了切线的判定和性质、圆周角定理的推论、正方形的性质和判定、相交弦定理、勾股定理和切割线定理．