题目内容
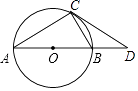
【题目】如图,AB为⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A重合),过点P作AB的垂线交BC于点Q. 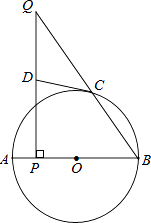
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.
(2)若cosB= ![]() ,BP=6,AP=1,求QC的长.
,BP=6,AP=1,求QC的长.
【答案】
(1)解:CD与⊙O相切.理由如下:
连结OC,如图,
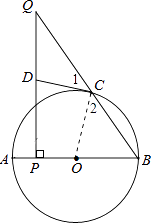
∵OC=OB,
∴∠2=∠B,
∵DQ=DC,
∴∠1=∠Q,
∵QP⊥PB,
∴∠BPQ=90°,
∴∠Q+∠B=90°,
∴∠1+∠2=90°,
∴∠DCO=180°﹣∠1﹣∠2=90°,
∴OC⊥CD,
而OC为⊙O的半径,
∴CD为⊙O的切线;
(2)解:连接AC,如图,
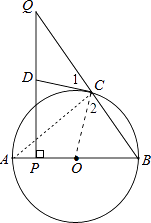
∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,cosB= ![]() =
= ![]() =
= ![]() ,
,
而BP=6,AP=1,
∴BC= ![]() ,
,
在Rt△BPQ中,cosB= ![]() =
= ![]() ,
,
∴BQ= ![]() =10,
=10,
∴QC=BQ﹣BC=10﹣ ![]() =
= ![]() .
.
【解析】(1)连结OC,由OC=OB得∠2=∠B,DQ=DC得∠1=∠Q,根据QP⊥PB得到∠Q+∠B=90°,则∠1+∠2=90°,再利用平角的定义得到∠DCO=90°,然后根据切线的判定定理得到CD为⊙O的切线;(2)连结AC,由AB为⊙O的直径得∠ACB=90°,根据余弦的定义得cosB= ![]() =
= ![]() =
= ![]() ,可计算出BC=
,可计算出BC= ![]() ,在Rt△BPQ中,利用余弦的定义得cosB=
,在Rt△BPQ中,利用余弦的定义得cosB= ![]() =
= ![]() ,可计算出BQ=10,然后利用QC=BQ﹣BC进行计算即可.
,可计算出BQ=10,然后利用QC=BQ﹣BC进行计算即可.
【考点精析】关于本题考查的切线的判定定理和解直角三角形,需要了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.

【题目】在汶川地震十周年纪念日,某教育集团进行了主题捐书活动,同学们热情高涨,仅仅五天就捐赠图书m万册,其中m与![]() 互为倒数.此时教育集团决定把所捐图书分批次运往市区周边的“希望学校”,而捐书活动将再持续一周.下表为活动结束前一周所捐图书存量的增减变化情况(单位:万册):
互为倒数.此时教育集团决定把所捐图书分批次运往市区周边的“希望学校”,而捐书活动将再持续一周.下表为活动结束前一周所捐图书存量的增减变化情况(单位:万册):
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 |
+0.2 | +0.1 | ﹣0.1 | ﹣0.4 | +0.3 | +0.5 | ﹣0.1 |
(1)m的值为 .
(2)求活动结束时,该教育集团所捐图书存量为多少万册;
(3)活动结束后,该教育集团决定在6天内把所捐图书全部运往“希望学校”,现有A、B两个运输公司,B运输公司每天的运输数量是A运输公司的1.5倍,学校首先聘请A运输公司进行运输,工作两天后,由于某些原因,A运输公司每天运输的数量比原来降低了25%,学校决定又聘请B运输公司加入,与A运输公司共同运输,恰好按时完成任务,求A运输公司每天运输多少万册图书?